Du mécanisme probable de la dépendance de fréquence

En se basant sur l'approche semi-classique, tachons d'évaluer la $c(\omega)$-dépendance par analogie avec l'optique. En fait c'est une des hypothèses éventuelles de la propagation des oscillations dans le vide. Décrivons le vide comme un système consistant de paires virtuelles (qui n'existent pas en réalité) "particule-antiparticule". Quand les particules réelles sont absentes, les particules virtuelles ne se manifestent pas (n'existent pas en réalité) dans le vide. Des oscillations des paires virtuelles apparaissent dans le domaine de la propagation de la lumière. La propagation de la lumière peut être décrite comme un processus de l'interaction consécutive avec des paires virtuelles (l'excitation vibrationnelle). Des paires virtuelles les plus légères positron - électron exercent la plus grande influence (des oscillations s'excitent facilement). C'est pourquoi on ne prendra en compte que ces paires-là.

Vu que des oscillations dans un atome ou un positronium sont des exemples des oscillations des particules réelles, elles ne peuvent pas déterminer la fréquence propre des oscillations des paires virtuelles. Il existe la seule fréquence pouvant correspondre à une paire virtuelle (qui n'existe pas hors de l'excitation). La fréquence propre peut être déterminée comme une fréquence, correspondant à la naissance d'une paire électron-positron $\omega_0=2m_ec^2/\hbar$, où $m_e$ est la masse d’un électron. En se basant sur cette description il est raisonnable de supposer que et l'électron et le positron dans le paire virtuel localisés dans le même point (le paire n'existe pas en réalité, ce qui provoque l’annihilation complète). En utilisant le modèle classique des oscillateurs, on peut inscrire la formule de la vitesse de la lumière de phase suivante:

$$c(\omega) = {c_0\over\sqrt{\varepsilon}}, ~~~~~~ \sqrt{\varepsilon} = n - i\chi,$$ (B.1)

$$n^2 - \chi^2 = 1 + 4\pi {Nfe^2/m_e\over (\omega_0^2-\omega^2)^2 + 4\omega^2\gamma^2}(\omega_0^2-\omega^2),$$

$$n\chi = 4\pi {Nfe^2/m_e\over (\omega_0^2-\omega^2)^2 + 4\omega^2\gamma^2}\omega\gamma.$$

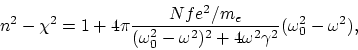
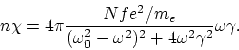
Il reste de déterminer les grandeurs $c_0$, $\gamma$ et $Nf$. Quant au choix de la grandeur $\gamma$, tout est claire: elle se détermine par le freinage de l'émission (l'unique choix possible dans le vide):

$$\gamma = {e^2\omega^2\over 3m_ec^3}.$$

Mais nous ne pouvons étudier que les domaines, où l'électrodynamique classique n'est pas intérieurement contradictoire et les effets des quanta de sont pas considérables, c'est-à-dire $\omega\ll\omega_0/137$ et $\lambda\gg 3.7\times 10^{-11}$ cm $\gg R_0$, où $R_0=e^2/(m_{e}c^2)$ est le rayon de l'électron. La grandeur $Nf$ signifie le nombre de paires virtuelles dans une unité de volume, qui est satisfaisant pour assurer le processus de la propagation de la lumière. En effet il s'agit de la détermination des dimensions d'un quantum de la lumière et du nombre de paires virtuelles, qui y ont lieu. Il est évident que le degré des dimensions longitudinales d'un quantum $l\sim \lambda$. Pour assurer la continuité des changements des champs ${\bf E}$ et ${\bf H}$, on peut supposer que la "substance" d’une paire virtuelle est "étalée" le long d’un quantum (à voir la Figure B.1) et tourne autour de l'axe local (perpendiculaire à l'axe du dessin et traversant l'axe $C$) avec la fréquence $\omega$.

Figure B.1: La propagation de la lumière en tant qu'une polarisation consécutive du vide.

Le domaine, occupé par une paire a des dimensions: $(2R_0,2R_0,R_l)$, où $R_l=\lambda/I$, $I$ est le nombre de paires "étalées". Etant donné que l'énergie cinétique moyenne (l'énergie du champ magnétique) est égale à l'énergie potentielle moyenne (l'énergie du champ électrique), le nombre $I$ peut être trouvé de l'égalité $2Ie^2/(2R_0)=\hbar\omega$. Alors

$$R_l = {2\pi ce^2\over \hbar\omega^2R_0}, ~~~~~ Nf = {\hbar\omega^2\over 8\pi ce^2R_0},$$

et la formule approximative finale pour la vitesse non dimensionnelle de phase de la lumière s'inscrit sous la forme suivante:

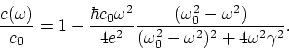$${c(\omega)\over c_{0}} = 1 - {\hbar c_{0}\omega^{2}\over 4e^... ...r (\omega_{0}^{2} - \omega^{2})^{2} + 4\omega^{2}\gamma^{2}}.$$ (B.2)

D'où est évident que $c_0=c(0)$. La vitesse de la lumière de phase diminue avec l'augmentation de la fréquence.

Faisons des certaines évaluation (à voir (B.2)). Pour le domaine ultraviolet: $(\Delta c/c_0)\sim -0.5\times 10^{-6}$ (dans le domaine visible l'effet a une valeur négligeable). Avec $\omega\sim 10^{18}$ secondes l'effet $(\Delta c/c_0)\sim -1.4\times 10^{-5}$. A cause de l'effet Doppler l'influence du mouvement de la Terre même pour le domaine ultraviolet provoque l'effet $(\Delta c/c_0)\sim -10^{-10}$ (à une valeur négligeable); à la frontière du domaine de l'application de cette description ($\omega\sim\omega_0/137$) recevons: $(\Delta c/c_0)\sim -3.6\times 10^{-7}$. En utilisant la formule $c^2k^2=\omega^2\varepsilon$, pour la vitesse collective $U_g=(d\omega/dk)$ recevons:

$$U_g{d(\omega\sqrt{\varepsilon})\over d\omega} = c_0.$$

La vitesse collective diminue aussi avec l'augmentation de la fréquence, presque coïncidente avec la vitesse de phase. Leur divergence la plus considérable est atteinte à la limite de l'application de cette description (pour $\omega\sim\omega_0/137$) et est égale à 0.01 de pour-cent (par rapport à $c_0$ environ $2\times 10^{-7}$). Notons aussi que des petites dimensions d'un quantum de la lumière utilisées ci-dessus, sont bien argumentées (selon des idées contemporaines). Un tel objet compact coopérera comme un tout et presque immédiatement avec n'importe quel objet du micro-univers, et en effet on est obligé de conditionner ces particularité dans la mécanique quantique (par exemple pour l'explication du photo-effet ou de l'effet Compton).

Les possibilités expérimentales généralement admises pour aujourd'hui sont insuffisantes pour la détermination de la $\omega$-dépendance de la vitesse de la lumière dans le domaine visible (comme et pour l'influence du mouvement de la Terre). Néanmoins, présentons certaines idées générales concernant des expériences. Il faut choisir l'objectif: découvrir la $\omega$-dépendance $c(\omega)$. Des mesurages doivent être directs, parce que n'importe quelle réévaluation entraîne des représentations théorétiques du processus considéré. En particulier, les expériences doivent être faites dans le vide, parce qu'un calcul purement théorétique de l’interaction de la lumière et de la substance ne peut pas être faits d’une manière exacte. Dans le cas général l'interaction avec la matière dépend de la fréquence de la lumière $\omega$. En particulier, des miroirs doivent refléter des ondes aux fréquences différentes $\omega$ différemment (de plus, la réflexion n'est pas un processus instantané). La démultiplication, liée avec la transformation de la lumière, ne prend pas en compte la $\omega$-dépendance éventuelle de la vitesse de la lumière. Dans le cas général l'interruption d'un rayon de la lumière transforme un groupe d'ondes et, par conséquent, sa vitesse. Comme des particules chargées libres peuvent influer sur l'effet, il est nécessaire d'éviter la protection métallique.

Le départ simultané des rayons avec des fréquences différentes et l'exactitude adéquate des laps de temps, auxquels une onde enveloppe passera une certaine distance, sont nécessaires pour la méthode des interruptions. Ou alternativement on peut exclure la ligne du spectre du mélange des deux lignes du spectre (des lasers) à l'aide de l'interruption. Vu que la réflexion n'est un processus immédiat et dépend de la fréquence de la lumière, la méthode habituelle de l'allongement de la distance à l’aide des miroirs ne convient pas, ou les nombres de réflexions pour chaque rayon de la lumière (pour chaque fréquence différente) doivent être égaux. La dernière remarque concerne aussi la méthode d’interférométrie. Divisons le rayon ($\omega_1$) en deux rayons. Le premier rayon se transforme (en $\omega_2$) à au début de la distance $L$; et le deuxième à la fin de la distance $L$. Supposons que $L$ peut être changée. Si la dépendance $c(\omega)$ existe, le champ d'interférences doit changer avec le changement de $L$. Pourtant il existe des difficultés techniques de changement de $L$ hors des fluctuations.

Des études spatiales d’un spectre assez large $\omega_i$ peuvent aider à découvrir la $c(\omega)$-dépendance. On peut observer d'un spoutnik l'apparition et la disparition non simultanées des formes spectrales caractéristiques dans deux systèmes pendant une éclipse totale. Cependant, quant aux grandes distances, on n'est pas réellement sur que la lumière passe à travers le vide (sans gaz, poussière, plasma etc.). Pour découvrir la $\omega$-dépendance $c(\omega)$ il faut faire l'analyse mathématique complémentaire $c(\omega_i)$ pour $\omega_i$.

La comparaison de $c(\omega)$ pour le domaine visible et pour des rayons X et des rayons gamma représente le plus grand intérêt. Autant qu'il est connu, il n’y a pas de donnés expérimentales pour ces domaines-là. Cependant il existe une série de difficultés des expériences avec des rayons gamma (à voir [7,59,67] pour la méthode des mesurages de $\lambda$ et $\nu$ la plus exacte pour le modèle d'ondes de la lumière), de plus, on n’est pas absolument sur de la nature ondulatoire de la lumière).

La question la plus générale de cette annexe est suivante: restent des particularités du vide sans changements lors de l'introduction des particules (des photons)? Si les particularités du vide changent, l'influence réciproque (le principe de l'interaction) sur le processus de la propagation des quanta (de la lumière) doit avoir lieu. La dépendance de $c(\omega)$ est une certaine manifestation de ce principe.

Donc, dans les annexes l'auteur a déduit les formules correspondant aux conséquences de la $c(\omega)$-dépendance, se rapportant à la TRR, à l'électrodynamique de quantum, à l'optique etc. La découverte de la $c(\omega)$-dépendance elle-même nécessite des études spéciales. L'effet maximal doit être observé dans un domaine à haute fréquence. Malgré des difficultés expérimentales graves, des éventuels résultats sont aussi importants qu'intéressants.

Un des mécanismes possibles, conduisant à la $c(\omega)$-dépendance pour le modèle d'ondes de la lumière a été analysé dans cette annexe. Mais notons qu'il n'y a pas d'expériences cruciales, démentant la loi classique de l'addition des vitesses même pour le modèle corpusculaire de la lumière, sans parler du modèle ondulatoire. C'est que pour la lumière trois dépendances suivantes sont sans doute liées dans le modèle ondulatoire de la lumière: la $c(\omega)$-dépendance, la loi Doppler et la loi de l'addition des vitesses. Et seule la connaissance des deux de ces trois dépendances sans doute détermine la troisième. Pour le modèle d'ondes le processus de la propagation des oscillations électromagnétiques (de la lumière) dans le vide peut être décrit comme l'apparition consécutive des oscillations des particules virtuelles - des paires), causée par la lumière diffusée elle-même. (Pour le bon, pour le modèle, analysé dans cette annexe, surgit la question des différences des particularités de la lumière, apparaissant lors de l'annihilation, des particules plus lourdes, et du rôle des autres paires virtuelles ou du "caractère élémentaire" des particules élémentaires).