Les annexes sont consacrées à l'étude de certaines hypothèses isolées. Elles ne sont presque pas liées avec la critique de la théorie de la relativité, présentée dans la principal partie du livre. Pourtant elles montrent la non-unicité de l'approche de la TRR et la possibilité de la fréquentielle paramétisation de tous les calculs. Dans ce livre les Appendices ne poursuivent aucun autre but, car les méthodes fausses de la TRR y sont utilisées (leur inconsistance a été prouvée dans les parties principales du livre). L'auteur a fait quelques tentatives d'exposer les idées présentées dans les deux premières appendices (plus une partie de l'analyse de l'expérience de Michelson de Chapitre 3) dans quelques revues bien connues de 1993 à 1999. Tantôt on diplomatiquement refusait tout d'un coup à la publication, tantôt on composait une réponse à peu près suivante: "Personne n'a vu rien de commun dans la théorie de la relativité et l'électrodynamique de quantum, et la précision des prédictions de ces théories est très haute". En général, comment un théoricien peut-il découvrir quelque chose de nouveau (au lieu de l'expliquer "postérieurement")? Il doit supposer un certain fait et vérifier les conséquences de sa supposition. Mais personne n'a tenté de supposer la possibilité de la dépendance fréquentielle de la vitesse de la lumière. De plus, il s'agissait de l'exactitude, dépassant l'exactitude contemporaine des expériences à 1-2 degrés. Une exactitude pareille peut être atteinte dans au plus proche délais, et dans la physique on sérieusement discute les expériences exigeant l'exactitude dépassant l'exactitude contemporaine aux dizaines de degrés. Enfin l'auteur s'est fatigué de gaspiller son temps et a décidé de comprendre ce que représente cette fameuse exactitude de la TRR (en se rappelant en outre, sa déception estudiantine de cette théorie). En résultat, le premier de ses propres articles critiques a apparu et aujourd'hui on peut le dire aussi par rapport à ce livre). Donc, n’importe quelle situation incorpore et des avantages et des défauts.
Passons maintenant à l'étude de la dépendance éventuelle de la vitesse de la
lumière de la fréquence. Il est connu que lors du passage des particules dans le
vide, des processus différents, comme l'apparition des paires virtuelles
(particule - antiparticule) y ont lieu; bien des processus de l'interaction
peuvent être décrits avec la participation de ces particules virtuelles. Lors de
sa propagation la lumière influence les particularités du vide (particulièrement
la polarisation du vide doit avoir lieu). Par conséquent selon le principe de la
réciprocité, l'influence réciproque du vide polarisé sur le processus de la
propagation de la lumière, doit exister. En résultat la lumière d'une certaine
fréquence se répand dans le vide comme dans le "milieu" avec une certaine
perméabilité ![]() , déterminée par la lumière diffusant lui-même,
c'est-à-dire
, déterminée par la lumière diffusant lui-même,
c'est-à-dire ![]() .
.
Il est connu que la généralisation des équations de Maxwell par moyen de
l'addition évidente de membre de masse dans le lagrangien de Maxwell amène aux
équations de Prokc dans l'espace de Minkovski (selon les idées contemporaines).
Les ondes électromagnétiques se diffusant dans le milieu, sont changé par le
milieu et cette influence se manifeste dans la production des photons massifs
[100]. Même si on suppose la constance de la vitesse de phase la dépendance de
fréquence (la dispersion dans le vide) de la vitesse collective de la lumière
surgit:
où, ![]() est la masse des quanta au repos. Pourtant dans ces annexes les questions de la
production de la masse et de la théorie d'une charge ne seront pas discutées.
L'objectif principal est d'étudier certaines questions physiques concernant la
vitesse de la lumière elle-même.
est la masse des quanta au repos. Pourtant dans ces annexes les questions de la
production de la masse et de la théorie d'une charge ne seront pas discutées.
L'objectif principal est d'étudier certaines questions physiques concernant la
vitesse de la lumière elle-même.
Les questions suivantes surgissent immédiatement: 1) Comment peut-on évaluer
et mesurer la ![]() -dépendance? 2) Pourquoi elle n'est pas encore découverte et 3) quelles
conséquences peut-elle produire?
-dépendance? 2) Pourquoi elle n'est pas encore découverte et 3) quelles
conséquences peut-elle produire?
Il existe des moyens différents du mesurage de la vitesse de la lumière, par
exemple: la méthode astronomique, la méthode de l'interruption, la méthode du
miroir tournant, la méthode radiogéodésique, la méthode des ondes stationnaires
(du résonateur), la méthodes des mesurages indépendants ![]() et
et ![]() . Aujourd'hui la
dernière méthode [59,67] est la plus exacte; c'est de cette méthode que le
Bureau des Normes mesure la vitesse de la lumière au huitième symbole près.
Pourtant il y a des difficultés de principe sur cette voie [7]. De plus, il est
à noter, que l'application de cette méthode est limitée par principe: elle peut
être liée à la vitesse de la lumière locale (à l'intérieur de l'appareil) ou
elle ne peut avoir aucuns liens avec la vitesse de la lumière, si la lumière ne
représente des ondes pures. Les causes de l'inexactitude des autres méthodes
(pour la découverte de la
. Aujourd'hui la
dernière méthode [59,67] est la plus exacte; c'est de cette méthode que le
Bureau des Normes mesure la vitesse de la lumière au huitième symbole près.
Pourtant il y a des difficultés de principe sur cette voie [7]. De plus, il est
à noter, que l'application de cette méthode est limitée par principe: elle peut
être liée à la vitesse de la lumière locale (à l'intérieur de l'appareil) ou
elle ne peut avoir aucuns liens avec la vitesse de la lumière, si la lumière ne
représente des ondes pures. Les causes de l'inexactitude des autres méthodes
(pour la découverte de la ![]() -dépendance) sont expliquées dans les Chapitres
précédents et pour une hypothèse isolée elles seront expliquées dans ces
annexes.
-dépendance) sont expliquées dans les Chapitres
précédents et pour une hypothèse isolée elles seront expliquées dans ces
annexes.
Ensuite nous allons suivre les méthodes de la TRR (oublions pour le moment
qu'elles sont fausses et ne donnent que "l'apparence" pour deux systèmes de
référence avec une condition complémentaire: l'application de la méthode de la
synchronisation d'Einstein). Rappelons que lors de la déduction des conséquences
de la TRR (par exemple, des lois des transformations) on utilise le concept de
l'intervalle ![]() . Ici il faut faire deux remarques méthodiques.
Même l'égalité des intervalles
. Ici il faut faire deux remarques méthodiques.
Même l'égalité des intervalles ![]() n'est qu'une des hypothèses
vraisemblables, car le seul point
n'est qu'une des hypothèses
vraisemblables, car le seul point ![]() reste sur (si on suppose
reste sur (si on suppose ![]() ). Par
exemple, on pourrait mettre au même niveau n'importe quels degrés de
). Par
exemple, on pourrait mettre au même niveau n'importe quels degrés de ![]() (
(![]() est un nombre
naturel):
est un nombre
naturel): ![]() et recevoir de différentes "lois physiques". Ou supposer
et recevoir de différentes "lois physiques". Ou supposer
![]() ,
mais
,
mais ![]() , c'est-à-dire
, c'est-à-dire ![]() (la vitesse apparente du mouvement réciproque est différente pour des
observateurs différents). Un tel choix provoque la coïncidence de l'effet
longitudinal relativiste de Doppler et la formule classique. Des systèmes
exotiques pareils peuvent être intérieurement coordonnés au même degré que la
TRR (c'est-à-dire seulement pour deux objets mis à part!) et seules les
expériences peuvent montrer lequel des choix n'est qu'une hypothèse théorétique.
L'auteur ne parlera pas ici de toutes les hypothèses exotiques pareilles.
(la vitesse apparente du mouvement réciproque est différente pour des
observateurs différents). Un tel choix provoque la coïncidence de l'effet
longitudinal relativiste de Doppler et la formule classique. Des systèmes
exotiques pareils peuvent être intérieurement coordonnés au même degré que la
TRR (c'est-à-dire seulement pour deux objets mis à part!) et seules les
expériences peuvent montrer lequel des choix n'est qu'une hypothèse théorétique.
L'auteur ne parlera pas ici de toutes les hypothèses exotiques pareilles.
Deuxièmement§ avec l'utilisation de l'intervalle on ne fait pas l'attention à
l'aspect suivant: on utilise la lumière concrète passant d’un point à un autre,
c'est-à-dire il faut y mettre la formule ![]() . Mais dans ce cas la proportionnalité des intervalles (tiré des
manuels) conduit au rapport vague:
. Mais dans ce cas la proportionnalité des intervalles (tiré des
manuels) conduit au rapport vague:
et même l'égalité des intervalles ne peut pas être argumentée. Le besoin des
expériences apparaît de nouveau, parce que ce rapport est lié avec la loi de
Doppler "inconnu" encore. Donc, les idées théorétiques, ne provenant que des
leurs propres principes, sont ambiguës. Vu que la conclusion généralement admise
de la TRR (la méthode) provoque des certaines conséquences, dites
expérimentalement prouvées (par exemple avec une certaine exactitude pour la
dynamique des particules?), appuyons-nous sur cette conclusion après l'avoir
transformée en prenant en compte la dépendance éventuelle ![]() .
.
Sa signification physique est suivante. Le résultat visible d'un mesurage
dépend de sa procédure, et le résultat de calcul, en particulier, de la méthode
de la synchronisation du temps pour des systèmes différents. Selon l'idée de
cette appendice "la vitesse unique du transfert des interactions
électromagnétique" n'existe pas (seulement ![]() existe). Si selon Einstein pour
la synchronisation des intervalles temporels on utilise la lumière d'une
certaine fréquence
existe). Si selon Einstein pour
la synchronisation des intervalles temporels on utilise la lumière d'une
certaine fréquence ![]() , le résultat des expériences dépendra de
, le résultat des expériences dépendra de ![]() . Par exemple, si
un certain processus avec la fréquence caractéristique
. Par exemple, si
un certain processus avec la fréquence caractéristique ![]() a lieu dans un
système, il est naturel d'étudier le système à l'aide de
a lieu dans un
système, il est naturel d'étudier le système à l'aide de ![]() (de la même
manière qu'un signal se répand). Si dans deux systèmes, qui se déplacent l'un
par rapport à l'autre, deux grandeurs apparaissent dans les formules:
(de la même
manière qu'un signal se répand). Si dans deux systèmes, qui se déplacent l'un
par rapport à l'autre, deux grandeurs apparaissent dans les formules: ![]() et
et
![]() pour chaque système, car la même lumière possède les fréquences
différentes dans les systèmes, se déplaçant l'un par rapport à l'autre. Dans ce
cas deux grandeurs
pour chaque système, car la même lumière possède les fréquences
différentes dans les systèmes, se déplaçant l'un par rapport à l'autre. Dans ce
cas deux grandeurs ![]() et
et ![]() sont liées suite à l'effet Doppler (à voir
ci-dessous). Il est intéressant de noter la circonstance suivante. Si dans un
système des processus avec les fréquences différentes
sont liées suite à l'effet Doppler (à voir
ci-dessous). Il est intéressant de noter la circonstance suivante. Si dans un
système des processus avec les fréquences différentes ![]() ont lieu, suite
aux
ont lieu, suite
aux ![]() -dépendances, les observateurs se déplaçant l'un par rapport à l'autre
verront des évènements différents dans le même point (l'effet visible). Dans les
explications suivantes nous allons suivre l'analogie avec [4,17].
-dépendances, les observateurs se déplaçant l'un par rapport à l'autre
verront des évènements différents dans le même point (l'effet visible). Dans les
explications suivantes nous allons suivre l'analogie avec [4,17].
Supposons que ![]() est une fréquence d'un signal qui se répand dans un
système. En mettant
est une fréquence d'un signal qui se répand dans un
système. En mettant ![]() (au lieu de
(au lieu de ![]() ) dans la formule de l'intervalle
) dans la formule de l'intervalle ![]() pour le système
propre et
pour le système
propre et ![]() dans
dans ![]() pour le système de référence, de
pour le système de référence, de ![]() vient que
le temps propre (
vient que
le temps propre (![]() ) peut être déterminé d'une manière suivante:
) peut être déterminé d'une manière suivante:
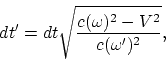 |
(A.1) |
et la formule pour la propre longueur reste en vigueur. Soulignons de nouveaux que tout cela n’est que des “effets de la visibilité”. Dans toute formule mathématique il est valable de transmettre des termes et des coefficients d’une partie de l’équation dans une autre selon de certaines règles (toutes formules pareilles sont équivalentes). Comment, donc, définir si le temps s’est accéléré chez l’un des observateurs ou s’il s’est ralenti chez l’autre (et la longueur s’est accrue ou diminuée)? Tout simplement, si on Vous disait que Votre temps s’est ralenti par rapport à un objet d’une manière et par rapport aux autres objets d’une autre manière, Vous sentiriez immédiatement le caractère délirant d’une quantité infinie de pareils “renseignements” inutiles. Mais quand les relativistes disent que chez Vous tout va bien et c’est que “quelque chose ne marche pas chez n’importe qui loin de Vous”, la plupart des gens finissent de s’inquiéter et continuent d’écouter des “contes”.
Utilisons la rotation ![]() pour la déduction des transformations de Lorentz:
pour la déduction des transformations de Lorentz:
Alors avec l'utilisation de ![]() les transformations de Lorentz
aboutissent à
les transformations de Lorentz
aboutissent à
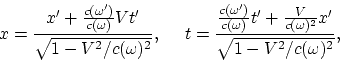 |
(A.2) |
où ![]() est une vitesse du système. En inscrivant
est une vitesse du système. En inscrivant ![]() et
et ![]() dans la formule (A.2) et en
déterminant
dans la formule (A.2) et en
déterminant ![]() , recevons les transformations de la vitesse:
, recevons les transformations de la vitesse:
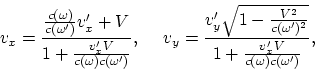
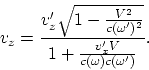 |
(A.3) |
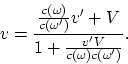 |
(A.4) |
On voit que la vitesse visible maximale est ![]() , où
, où
![]() est
la fréquence de la lumière dans le système propre. Remarquons, que toutes les
formules amènent à la loi correcte de la composition lors du mouvement le long
d'une droite (des transformations du système
est
la fréquence de la lumière dans le système propre. Remarquons, que toutes les
formules amènent à la loi correcte de la composition lors du mouvement le long
d'une droite (des transformations du système ![]() au système
au système ![]() et du
et du ![]() au
au ![]() donnent le même résultat que la
transformation de
donnent le même résultat que la
transformation de ![]() à
à ![]() ). Mentionnons que selon la partie principale du livre, les grandeurs
). Mentionnons que selon la partie principale du livre, les grandeurs
![]() et
et
![]() dans
les formules (A.1) et (A.2) ne possèdent pas de sens physique propre (elles sont
des grandeurs fictifs et complémentaires). La formule (A.4) par analogie avec la
formule (1.5), peut être réécrite en forme suivante
dans
les formules (A.1) et (A.2) ne possèdent pas de sens physique propre (elles sont
des grandeurs fictifs et complémentaires). La formule (A.4) par analogie avec la
formule (1.5), peut être réécrite en forme suivante
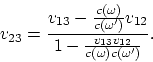 |
(A.5) |
En cette forme son essence (l’effet apparent) est la plus visible. La formule
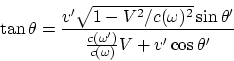 |
(A.6) |
décrit le changement de la direction de la vitesse. La formule relativiste
pour l'aberration de la lumière est gardée (la substitution ![]() ).
Mentionnons à tout hasard que la formule relativiste de l'aberration stellaire
est approximative. Les transformations des 4-vecteurs sont aussi gardées. D'où
vient la transformation du vecteur d'onde quatridimentionnel
).
Mentionnons à tout hasard que la formule relativiste de l'aberration stellaire
est approximative. Les transformations des 4-vecteurs sont aussi gardées. D'où
vient la transformation du vecteur d'onde quatridimentionnel ![]() :
:
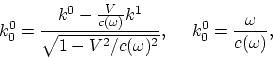
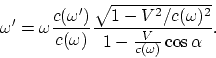 |
(A.7) |
Remarquons qu'il s’en suit la dépendance de la vitesse de la lumière (![]() )
du mouvement du système (aux systèmes différents correspondent les fréquences
différentes
)
du mouvement du système (aux systèmes différents correspondent les fréquences
différentes ![]() ). Pourtant cet effet est négligeable pour le domaine
optique (on en parlera dans l'annexe suivante). Les relativistes affirment que
la formule pour l’expression de l’effet Doppler inclut une vitesse relative.
Cela n’est pas correct. Supposons que dans un point sur la Terre une explosion a
eu lieu et une raie émise a apparu temporairement. Supposons qu’un récepteur sur
Pluton a capté le signal. Auquel moment faut-il définir cette vitesse relative
mythique? Car au moment de l’explosion le récepteur pourrait ne pas être tourné
vers la Terre tandis qu’au moment de la réception du signal la source n’existait
plus et la Terre s’est tournée du rebours? Même à l’absence du milieu au lieu de
la vitesse absolue on aurait la différence entre les vitesses absolues au moment
de l’émission et de la réception du signal (et ce ne sont pas les mêmes
choses!). Et c’est à l’expérience de montrer ce qu’il existe en réalité.
). Pourtant cet effet est négligeable pour le domaine
optique (on en parlera dans l'annexe suivante). Les relativistes affirment que
la formule pour l’expression de l’effet Doppler inclut une vitesse relative.
Cela n’est pas correct. Supposons que dans un point sur la Terre une explosion a
eu lieu et une raie émise a apparu temporairement. Supposons qu’un récepteur sur
Pluton a capté le signal. Auquel moment faut-il définir cette vitesse relative
mythique? Car au moment de l’explosion le récepteur pourrait ne pas être tourné
vers la Terre tandis qu’au moment de la réception du signal la source n’existait
plus et la Terre s’est tournée du rebours? Même à l’absence du milieu au lieu de
la vitesse absolue on aurait la différence entre les vitesses absolues au moment
de l’émission et de la réception du signal (et ce ne sont pas les mêmes
choses!). Et c’est à l’expérience de montrer ce qu’il existe en réalité.
Le vecteur de l'énergie-impulsion se transforme d'une manière suivante:
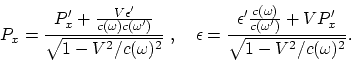 |
(A.8) |
Si on tombe d'accord avec l'idée de cette annexe, il doit exister une analogie plus proche entre la propagation de la lumière dans le milieu et dans le vide.
(1) Des différents groupes d'ondes se répandent dans le vide différemment.
(2) La dispersion de la lumière dans le vide limite le degré du parallélisme des rayons.
(3) Il y a la dissipation de la lumière dans le vide, c'est-à-dire l'intensité de la lumière diminue au fur et à mesure de sa propagation dans la vide.
(4) La lumière "vieillit", c'est-à-dire la fréquence de la lumière diminue avec sa propagation dans le vide. Ce phénomène peut être lié avec le paradoxe (d'Olberse) "pourquoi le ciel ne flambe pas?" et contribue au déplacement rouge, c'est-à-dire la correction de la conception du développement de l'Univers est possible. Etant donne qu'il s'agit en réalité de l'explication alternative du déplacement rouge, cet effet est minime et aujourd'hui il est impossible de le confirmer dans les études laboratoire: le déplacement rouge des courbes des objets spatiaux se détecte déjà par les méthodes classiques les plus exactes et il ne devient visible que pour des objets éloignés à la distance qui ne se détermine même pas par la base de l'orbite de la Terre (par le triangle); mentionnons à cette occasion que la grandeur de la constante de Habble a été déjà corrigée à un degré.
Avec le passage à l'électrodynamique de quantum on a besoin de la
substitution ![]() dans touts les calculs. Par exemple, cette
dépendance apparaît par rapport aux incertitudes
dans touts les calculs. Par exemple, cette
dépendance apparaît par rapport aux incertitudes
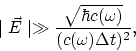
Les formules décrivant la ![]() -dépendance changent d'une manière visible. Comme
exemple considérons l'émission et l'absorption des photons. En résultat un
nouveau coefficient apparaît
-dépendance changent d'une manière visible. Comme
exemple considérons l'émission et l'absorption des photons. En résultat un
nouveau coefficient apparaît
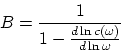
et dans des rapports des probabilités (de l'absorption, de l'émission forcée
et spontanée) ![]() . La grandeur
. La grandeur ![]() apparaît aussi dans des formules
des coefficients d'Einstein.
apparaît aussi dans des formules
des coefficients d'Einstein.
En utilisant la substitution ![]() pour les oscillations propres
du champ, recevons une formule pour des Fourier-components du propagateur des
photons:
pour les oscillations propres
du champ, recevons une formule pour des Fourier-components du propagateur des
photons:
Il est impossible de déterminer ![]() sans une dépendance visible
sans une dépendance visible ![]() . Une forme
évidente de la
. Une forme
évidente de la ![]() -dépendance est aussi nécessaire pour la déduction des
formules finales pour des sections différentes (dispersion, naissance de paires,
désintégration etc.). On peut faire la substitution
-dépendance est aussi nécessaire pour la déduction des
formules finales pour des sections différentes (dispersion, naissance de paires,
désintégration etc.). On peut faire la substitution ![]() dans des formules connues en tant de la première approximation.
dans des formules connues en tant de la première approximation.