The paradox of antipodes

The erroneousness of SRT is proved very simply by the whole life of mankind on the planet Earth. Let us consider the elementary logical contradiction of SRT - the paradox of antipodes. Two antipodes situated at the equator (for example, one person in Brazil, the other one - in Indonesia) differ by the fact, that due to the Earth rotation they move relative to each other at constant speed at each time instant (Fig. 1.5).

Figure 1.5: The paradox of antipodes.

Therefore, despite the obvious symmetry of the problem, each of these persons should grow old or grow young relative to another one. Does the gravitation hinder? Let's remove it and place each of our "astronauts" into a cabin. Each person can determine the time on such a "round robin" (as well as on the Earth) from the direction to the far star, which is motionless with respect to the round robin center, and from the period of intrinsic rotation of a round robin (a whirligig). The running of time will obviously be identical for both "astronauts". The time can be synchronized by the calculation technique knowing the period of revolution (all these problems are technological, rather than principal). Let's increase the linear speed $v\rightarrow c$ for amplifying the effect (for example, in order that according to SRT formulas the difference in time be "running up" 100 years for one year). Does the centrifugal force (acceleration) hinder? Then we shall increase radius $R$ of the round robin, so that $v^2/R\rightarrow 0$ (for example, in order that even for 100 years the overall effect from such an acceleration be many orders of magnitude lower, than the existing accuracy of its measurement). In such a case none of experiments can distinguish the motion of antipodes from rectilinear one, i.e. the system non-inertialness cannot be experimentally detected throughout the test. It is worthless for relativists to fight for the principal necessity of inertialness of the system. Recall that even in such the strict science as mathematics (in the justification of the theory of real numbers, for example), it is used the notion of the number $\varepsilon$ given beforehand, which can be chosen as small as one likes. In case discussed for the strict mathematical transition, the ratio of a centrifugal acceleration $v^2/R$ to the Earth's centrifugal acceleration $a_{c}$ can be made less than any arbitrary value of $\varepsilon$ at the expence of a large radius of a "round robin" $R$ (for instance, we can choose $\varepsilon\sim 10^{-10}$ or $\varepsilon\sim 10^{-100}$, whereas all SRT experiments were made on the Earth with $\varepsilon\sim 1$!). And, further, if you trust in the relativity (either according to SRT or according to Galileo - indifferently, since we compare time durations), then you can transfer the motion of one of antipodes, in a parallel manner, closer to the other antipode and forget about the round robin model at all. Obviously, the reverse mental operation can always be performed for any two mutual opposite motions with the same speed as well. Namely, we can perform parallel transfer of one of trajectories to a great distance $R\rightarrow\infty$ and "bridge" the motions by some "round robin". So, will "the patient be alive or dead" after some years? And who is more pleasant for you - the Brazilian or Indonesian? The full symmetry of the problem and full failure of SRT! Note, generally speaking, that the unique character of time cancels the principality of the issue of its synchronizing: the watch can, for example, be worn with yourself. Some doubts on "near inertial" motions will be discussed below in Chapter 3. If some relativists will on principle try to connive (themselves and somebodies) at the possibility of such a transition to a large R, we can offer to inscribe a regular n-gon into a circle of the large R (n > 2; stationary observers are placed at all angles) and to consider pure rectilinear motions of spacecrafts with astronauts along the sides of the n-gon. Even the same loops for using the same "earth" acceletations g (to gather the equal large speeds) can be joined to the angles of the n-gon in the identical manner. Obviously, all these inertial systems of the spacecrafts are absolutely identical for a stationary observer (at the center of the circle, for example). The course of time is the same for all spacecrafts in spite of different relative motions of the spacecrafts.

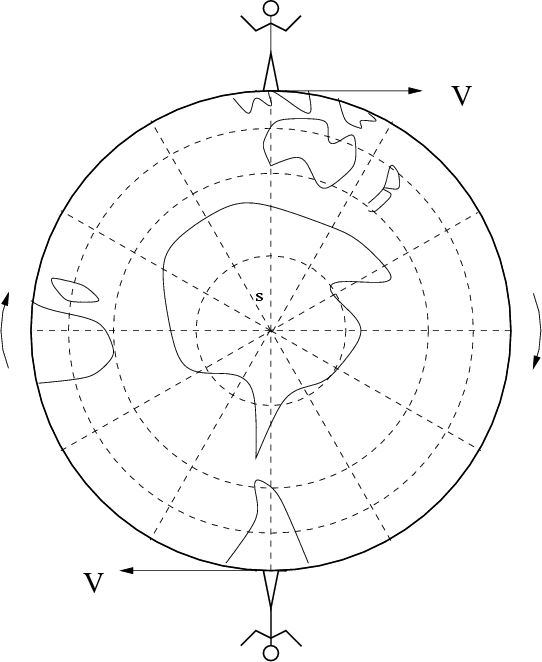
We can also draw the obvious symmetric scheme of "a flower type" with the possibility of the simultaneous start and finish of astronauts at the center of a circle (see Fig.~1.6).

Figure 1.6: The symmetric model of "a flower".

Since we will compare the time course (but not time beginning), we can use the equality of the time course for any two mutually resting objects. Then, the model of a whirligig can be easily generalized to the case of arbitrary (in directions and values) velocities of objects. This is purely geometric trivial problem (Fig. 1.7).

Figure 1.7: The model of a whirligig for arbitrary planar motions.

For example, let us have two motions, which are pictured in Fig. 1.7 with the velocity vectors $\overrightarrow{AA_1}$ and $\overrightarrow{BB_1}$. The both velocities possess the same modulo $v$ which tends to the speed of light $v\rightarrow c$. Let us choose an arbitrary point $O$ in the space. Furthermore, we draw a circle with the center at the point $O$ and such a radius $R$ that the centrifugal acceleration will be less than some preassigned small value $\varepsilon_1$ (an existing accuracy of measurement of accelerations, for example): $v^2/R < \varepsilon_1$, i.e. $R > v^2/\varepsilon_1$. We draw the straight line $AA_2$ which is perpendicular to the straight line $AA_1$. Thereafter, we draw the line $A_3A_4$ passing through $O$ and parallel to $AA_2$. At a point of intersection of this line and the circle we draw the velocity vector $\overrightarrow{A_3A_5}$ which is parallel to $\overrightarrow{AA_1}$ and has the same absolute value $\vert\overrightarrow{AA_1}\vert$. Factually, we simply made a parallel translation of the motion with velocity $\overrightarrow{AA_1}$. Making the analogous procedure with the motion $\overrightarrow{BB_1}$, we obtain motion with velocity $\overrightarrow{B_3B_5}$. Now both the motions are placed at the same circle and they cannot be distinguished from inertial motions with an existing accuracy. Due to obvious symmetry of the problem, the time course will be the same for these objects. For example, the time course can be measured with periodic flashes, which occur at the center $O$ of the circle. Now we take motion with the velocity vector $\overrightarrow{CC_1}$. It is parallel to $\overrightarrow{AA_1}$, but possesses some other absolute value. We make a parallel translation of $\overrightarrow{CC_1}$ and obtain $\overrightarrow{C_3C_5}$ (here we take the radius $\vert OC_3\vert=R\vert\overrightarrow{C_3C_5}\vert/\vert\overrightarrow{A_3A_5}\vert$). In this case we see that two objects (with velocities $\overrightarrow{A_3A_5}$ and $\overrightarrow{C_3C_5}$) will move along concentric arcs of circles $A_3a$ and $C_3d$. These objects will remain at the same distance from each other along the radii of the circles. (Some big arcs are shown here for visualization only, i.e. all angular values are increased; in fact, all arcs will be very small and indistinguishable from rectilinear segments.) It is obvious that the time course for such objects will be the same. Time can again be "measured off" by periodic flashes from the center O (number of light spheres which are passed through the circle $C_3d$ is the same as for the circle $A_3a$: the light spheres do not "disappear, condense, add, or hide themselves" anywhere). We can also draw the circle through the point $C_3$ and at any new point draw the tangential velocity vector $\overrightarrow{D_3D_5}$ with the same absolute value $\vert\overrightarrow{C_3C_5}\vert$. Again, the objects with velocities $\overrightarrow{D_3D_5}$ and $\overrightarrow{C_3C_5}$ are placed at the same circle, and, due to the symmetry of the problem, the time course will be the same. Thus, on the example of motions with velocities $\overrightarrow{A_3A_5}$ and $\overrightarrow{D_3D_5}$ (or $\overrightarrow{B_3B_5}$ and $\overrightarrow{C_3C_5}$) we proved that the time course is independent on both the absolute value and the direction of the velocity of objects, but it is the same. Passage to the three-dimensional case is trivial. At the first, we will transfer the beginning of one velocity vector to the beginning of the second velocity vector. Thereafter, we can draw a plane through these intersecting straight lines. In this plane we can carry out all previously described constructions. Thus, the time course is independent on any motions of inertial systems.