The theory of collisions and the conservation laws in SRT

Very frequently in SRT, for "simplifying" the description of collisions, the technique of transition to any "conveniently moving" frame of reference is used. Such a procedure, however, has no physical grounds, and the principle of relativity for closed identical systems is for nothing here at all. If the relativistic experiments are carried out on artificial beams of particles, then the sources (accelerators) and recording instruments are bound to the Earth, and accelerators and instruments will not fly, together with a moving observer, from our mental imagination only. If some process in Wilson's chamber is investigated, then the tracks of particles are bound to a medium (that is, to Wilson's chamber), rather than to a flying observer. For example, in the classical physics the angle between the tracks of particles will not change due to motion of an observer. At the same time, the angle between the velocities of particles, which leave mentioned tracks, can depend on observer's motion velocity. In the relativistic physics the angles between trajectories and between velocities of particles depend, also according to various laws, on observer's motion velocity. Therefore, such a seemingly probable from SRT viewpoint transition to a new frame of reference can essentially distort the interpretation of a solution. That is, any process should be considered in the frame of reference of a real observer (or recording instrument) only.

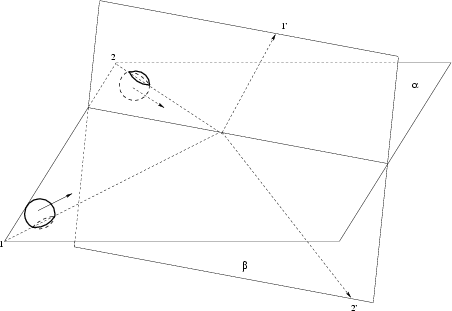
One more distortion of reality is the consideration of the process of collision of two particles (being principally point-like in SRT) as a planar motion. In fact, to fit to an ideal problem of two points, a measuring device cannot simultaneously fly with each pair of particles and differently rotate even in studies of statistical characteristics of point particles: the position of the device is fixed. Besides the point-like particles should be considered as a limiting case of particles having real finite size (otherwise no frontal collisions would be observed, it would be impossible to consider collisions of atoms and molecules, the protons would not have structure, etc.). And in the present case the collision of particles is principally three-dimensional (the probability of planar motion is zero). Let, for example, two identical balls (1 and 2) to approach each other before collision over straight lines crossing in space (the minimum distance between skew straight lines is smaller than the ball diameter). Even from the very beginning of the experiment we cannot draw the plane through these specified straight lines. Nevertheless, we shall take the middle of a minimum distance between crossing straight lines (the trajectories before collision) and draw through it intersecting straight lines parallel to the given trajectories.

Figure 4.8: Nonplanar motion of two particles.

Now, only one plane $\alpha$ passes through intersecting straight lines (Fig. 4.8). The centers of balls move parallel to this plane before collision: the first ball's center moves slightly above the plane and the second ball's center - slightly below this plane. After collision the balls will fly over other crossing straight (skew) lines. And, again, it is impossible to draw the plane through these skew straight lines. Again, we shall perform a similar procedure with parallel transition of straight lines, on which the lines of motion lie after collision, before intersecting at the middle. We shall draw through intersecting straight lines the plane $\beta$ (the centers of balls will again move on different sides from this plane). However, "the plane before collision" does not coincide with "the plane after collision", but intersects it at some angle.

Second method: let us draw one plane $\gamma$ through the trajectory of motion of the first particle (intersecting straight lines of its motion before and after collision), and the second plane $\delta$ - through a similar trajectory of motion of the second particle. However, these planes are also intersected at some angle (Fig. 4.9).

Figure 4.9: Three-dimensionality of collision of two particles.

So, what follows from three-dimensionality of motion? First. Not all relations turn out linear ones. For example, the distance between bodies occurs some nonlinear function of time even for the rectilinear uniform motion of the bodies along skew lines. Second. We shall write the classical laws of conservation of momentum (in projections) and of energy:

$$v_{1x} + v_{2x} = v'_{1x} + v'_{2x}$$ (4.3)

$$v_{1y} + v_{2y} = v'_{1y} + v'_{2y}$$ (4.4)

$$v_{1z} + v_{2z} = v'_{1z} + v'_{2z}$$ (4.5)

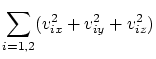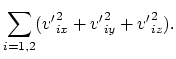$$\sum_{i=1,2}(v^2_{ix} + v^2_{iy} + v^2_{iz}) = \sum_{i=1,2}({v'}^2_{ix} + {v'}^2_{iy} + {v'}^2_{iz}).$$ (4.6)

We see from (4.3-4.6), that for six unknown quantities ($v'_{1x}, v'_{1y}, v'_{1z}, v'_{2x}, v'_{2y}, v'_{2z}$) there are four equations only. Thus, there should remain two indefinite parameters in the solution. If we suppose the motion to be planar (i.e. exclude equation (4.5)), then for remaining four unknowns we shall have three equations. Therefore, in comparing SRT results with the classical physics the substitution of solutions is accomplished, and there remains only one indefinite parameter (the scattering angle is usually considered to be the latter one). Such a substitution results in improper interpretation of the experimental data, especially when the missed quantities are restored. For example, the book [33] demonstrates two tracks of fly-away of particles of identical mass and charge (more correctly, of identical $e/m$ ratio) with dispersion angle lower than $90^{\circ}$, and the conclusion on the classical mechanics invalidity is drawn from this demonstration. Let us write the expression for angle $\alpha$ between the trajectories of dispersed particles:

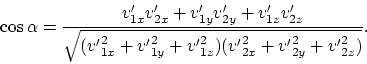$$\cos\alpha = {v'_{1x}v'_{2x} + v'_{1y}v'_{2y} + v'_{1z}v'_{2... ...1y} + {v'}^2_{1z})({v'}^2_{2x} + {v'}^2_{2y} + {v'}^2_{2z})}}.$$ (4.7)

Choose axis $Z$ so, that it will be $v_{1z}=v_{2z}=0$. Now we express variable $v'_{1x}$ from equation (4.3), variable $v'_{1y}$ - from equation (4.4), variable $v'_{1z}$ - from equation (4.5), and from equation (4.6) we shall express quantity ${v'}^2_{2z}$ (in this case the condition ${v'}^2_{2z} > 0$ restricts the region of possible values of all variables). Substitute all aforementioned quantities into equation (4.7). As a result, we obtain the two-parametric dependence on $v'_{2x}$ and $v'_{2y}$, which is not written here because of its awkwardness. Using graphical programs, we can be convinced that for the given values of $v_{1x}, v_{1y}, v_{2x}, v_{2y}$ we obtain some surface similar to the inner part of a cylinder; that is, quantity $\cos\alpha$ varies within wide limits. For example, it can easily be verified that the values

$$v_{1x}=0,1; ~ ~ ~ v_{1y}=0,1; ~ ~ ~ v_{2x}=0,7; ~ ~ ~ v_{2y}=0,7; ~ ~ ~ v'_{1x}=0,6;$$

$$v'_{2x}=0,2; ~ ~ ~ v'_{1y}=0,4; ~ ~ ~ v'_{2y}=0,4; ~ ~ ~ -v'_{2z}=v'_{1z}=\sqrt{0,14}$$

satisfy all classical conservation laws (4.3-4.6). For these values we obtain $\cos\alpha = 0.29554$, that is, $\alpha\approx 72.8^{\circ}$. Note: if the velocities are assumed to be expressed in terms of the speed of light, then a lower velocity is quite real for the motion of internal electrons in atoms beginning with $z\ge 60$. And, generally, nobody saw electrons in atoms being at rest! The angle of $90^{\circ}$ is unambiguously obtained in the classical physics at collision with a particle being at rest in the coordinate system of a recorder (but only where such a particle can be found?). However, the observed fly-away angle of $90^{\circ}$ does not result at all in an unambiguous opposite assertion, that one of particles had been at rest (the mathematical probability of such an event is infinitesimal). Thus, the reverse problem of restoring the missed data is not an unambiguous procedure either in the classical, or in the relativistic physics (there exists an infinite number of various self-consistent solutions).

For more rigorous verification of conservation laws in collisions (independent on any theory) it is necessary to study collisions of particles in vacuum for narrow monoenergetic beams of known particles for the given collision angles. In this case the complete study of the collision process should include the check of the energy balance of particles (for each scattering angle in space), the testing the balance of momenta of particles, the testing the balance of the total number of particles in beams before and after collision (the probability of scattering), the control of the balance of arising radiation in energies and directions. There are two more questions (two more uncertainties), which are not usually emphasized, namely: does the scattering depend on a mutual orientation of spins of colliding particles? And do these spins change during the collision? In the classical physics the answer to these questions is "yes" (but in the quantitative respect it strongly depends on the "structure" of balls).

The author did not meet any complete analysis of any collision process in SRT with respect to all issues set forth above. This does not imply, however, an unambiguous conclusion on invalidity (within the limits of experimental errors) of usually utilized relativistic conservation laws in any collision process (though this can quite occur to be the fact for many separate cases). The author only asserts that there are no even separate examples of absolute confirmation of relativistic collision laws (to say nothing of the global confirmation).

From a principally rigorous position, the application of relativistic conservation laws to the collision process in the elementary particle physics is rather doubtful. Whether these laws can retain their form irrespective of the charge of colliding particles, collision angles and dispersion angles? You see, the charged particles undergo acceleration during the collision. Therefore, in the modern concepts (in the SRT as well), some radiation (field) should always be observed. Is it necessary, really, to behave as the students having peeped at the answer to the problem: if the instrument has recorded a $\gamma$-quantum ("has seized our hand"), then it should be clearly taken into account "with a clever air". And should one trust in validity of SRT formulas "with a clever air" in remaining cases as well? So, where is the "predictive force" of SRT? Actually, the conservation laws should be explicitly supplemented by the terms, which take into account the energy and momentum of the field.

Generally speaking, the only case, where the discussion of relativistic conservation laws at "collisions" is lawful, is the interaction of particles with the forces of electromagnetic nature (the Lorentz force). For remaining cases the fulfillment of relativistic conservation laws is an unverified hypothesis (the light spheres of SRT bear no relation to the forces of non-electromagnetic nature). However, in the case of electromagnetic interactions no SRT ideas are required for deriving relativistic conservation laws as well. It is known that the equations of motion with the initial conditions completely determine all characteristics of motion, including the integrals of motion. Such an integral of motion can be the energy (but not always!). It follows from the equation of motion, that

$${d{\bf P}\over dt} = {\bf F} ~ ~ \Rightarrow ~ ~ {\bf v}d{\bf P} = {\bf F}d{\bf r}.$$ (4.8)

Introduce the definition of the potential energy

$$U = - \int_{r_0}^r {\bf F}d{\bf r}.$$

Knowing the form of the momentum (this is a quantity appeared in the experimental equation of motion (4.8); for example, in the classical case ${\bf P} = m{\bf v}$ and in the relativistic case ${\bf P} = m{\bf v}/\sqrt{1-v^2/c^2}$), one can obtain the energy conservation law from $dE={\bf v}d{\bf P} - {\bf F}d{\bf r}$: classical $U+mv^2/2=constant$, or relativistic $U+mc^2/\sqrt{1-v^2/c^2}=constant$, respectively. Under the condition of equality forces of action and counteraction (the third Newton's law, the hypothesis of central forces) we have: ${\bf F}_{12}=-{\bf F}_{21}$. Then from the equation of motion (4.8) we can obtain the momentum conservation law (this is again a quantity appeared in the experimental equation of motion (4.8)): from $d{\bf P_1}/dt={\bf F}_{12}, d{\bf P_2}/dt={\bf F}_{21}$ we obtain

$${d({\bf P}_1+{\bf P}_2)\over dt} = 0, ~ ~ \Rightarrow ~ ~ {\bf P}_1+{\bf P}_2=constant.$$

However, in the presence of magnetic forces ${\bf F}_{12}\ne -{\bf F}_{21}$, and the relativistic law of conservation of momentum of particles can be violated in the general case. Since the majority of particles, even many electrically neutral ones, have magnetic moment (i.e. they represent not "ideal point charges of the SRT", but charged magnetic rotators of finite size), the application of the relativistic momentum conservation law in the nuclear physics and elementary particle physics without explicit considering the field momentum is completely illegitimate. Therefore, we again arrive at the necessity of explicit considering the momentum (and, hence, the energy) of the field at collisions. (Possibly, this will help to regulate the nuclear physics and elementary particle physics and to decrease the number of particles-ghosts?)

The account taken of the radiation reaction force also results in violation of energy and momentum conservation laws declared in SRT. Should we refuse from accounting this force in the process of collision of particles? But this force just should be most significant in this process (there are great fields, owing to rapprochement of high-energy particles, and great variable accelerations).