The equivalence principle

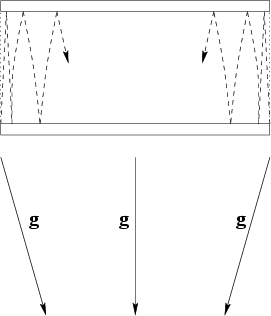
Now we shall turn to the next important GRT notion - the equivalence of the gravitational field to some system non-inertiality. In contrast to any non-inertial system, the gravitational field possesses some unique property: all moving objects deflect in it toward a single center. If we generate two light beams between two ideal parallel mirrors and direct them perpendicular to mirrors, then in the inertial system these beams will move parallel to each other for infinitely long time. A similar situation will take place at acceleration in the non-inertial system, if the mirrors are oriented perpendicular to the direction of acceleration. And, on the contrary, in the gravitational field with similar orientation of mirrors the light beams will begin to approach each other (Fig. 2.5).

Figure 2.5: Rapprochement of parallel light beams in the gravitational field.

And, if some effect will happen to be measured during the observation, then, owing to a great value of light speed, the existence of namely the gravitational field (rather than the non-inertiality) can also be identified. Obviously, the curvature of mirrors should not be taken into consideration, since, along with gravitational forces there exist also the other forces, which can retain the mutual configuration of mirrors. The distinction of a spherical symmetry from planar one can be found for weak gravitational fields as well. The GRT conclusion on the possibility of excluding the gravitational field for some inertial system during the whole observation time is wrong in the general case.

The equivalence principle of the gravitational field and acceleration can be related to one spatial point only, i.e. it is unreal: it leaded to a false result for the light beam deflection in the gravitational field, for example (only later Einstein corrected the coefficient in two times). The equivalence principle of the inertial and gravitating mass can be rigorously formulated also for a separate body only (it is unreal for GRT, since GRT involves interdependence of the space-time and all bodies). Because of this, GRT does not physically proceed to any non-relativistic theory at all (but formally mathematically only). All relativistic linear transformations can be related to empty space only, since real bodies (even simply as reference points) lead to nonlinear properties of the space. Then, phenomena differences with changing reference systems must be studied for the same point (in the space and time). But how can two different observers be placed at one point? Therefore, the relativistic approach can possess the approximate model character only (without globality).

It is not any surprising thing, that the same physical value - a mass - can participate in different phenomena: as a measure of inertia for any acting forces, including the gravitational one, and as a gravitating mass (for example, a moving charge produces both electric and magnetic fields). The question on the rigorous equality of inertial and gravitating masses is entirely artificial, since this equality depends on the choice of a numerical value of the gravitational constant $\gamma$. For example, expressions (laws) retain the same form in the case of proportionality $m_g = \alpha m_{in}$, but the gravitational constant will be defined as $\gamma' = \alpha^2\gamma$. It is not necessary to search any mystics and to create pictures of curved space. The substitution of the same value for the inertial and gravitating mass is made not only for GRT, but for the Newton's theory of gravitation as well. It is nothing more than an experimental fact (more precisely, the most simple choice of the value $\gamma$).

When one comes to the dependence of a form of equations on space-time properties [37], there exists some speculation for this idea. The impression is given that we can change this space-time to check the dependence claimed. In fact, the Universe is only one (unique). GRT tries to add a complexity of the Universe to any local phenomena, which is not positive for science. The choice of local mathematical coordinates is a different matter (a phenomenon symmetry can simplify the description in this case) and globality is not the case again.

The use of non-inertial systems in GRT is contradictory intrinsically. Really, in a rotating system rather distant objects will move at velocity greater than light speed; but SRT and GTR assert, that the apparent velocities should be lower, than $c$. However, the experimental fact is as follows: the photograph of the sky, taken from the rotating Earth, indicates, that the visible solid-state rotation is observed. The use of a rotating system (the Earth, for example) does not contradict the classical physics at any distance to the object from the center, whereas in GRT the value of $g_{00}$ component becomes negative, but this is inadmissible in this theory. What's about astronomical observations?