La lois relativiste de l’addition des vitesses

Rappelons que la cinématique ne s’occupe pas de la recherches des causes du mouvement, mais affirme, par exemple le suivant: si les vitesses sont données, alors on peut calculer le résultat de l’addition des vitesses. Les questions de la dynamique des particules (qui s’occupe de causes du mouvement) exigent de l’examination séparée (regardez le Chapitre 4).

Faisons maintenant une remarque au sujet de la loi relativiste de l’addition des vitesses. Pour les deux systèmes qui participent directement dans le mouvement relatif aucune doute n’apparaît devant la définition de leur vitesse relative (ni dans la physique classique, ni dans la théorie de la relativité restreinte). Supposons qu’un système $S_2$ se déplace relativement au système $S_1$ à la vitesse $v_{12}$; par analogie le système $S_3$ se déplace relativement au système $S_1$ à la vitesse $v_{13}$. De fait, la loi relativiste de l’addition de vitesses détermine la vitesse relative du tel mouvement, dans lequel l’observateur ne participe pas lui-même. La vitesse du mouvement du système $S_3$ relativement à $S_2$ se définira comme ça:

$$v_{23} = {v_{13} - v_{12}\over 1 - {v_{13}v_{12}\over c^2}}.$$ (1.5)

Précisément sous cet aspect (bien que d’habitude on exprime $v_{13}$ à l'aide de $v_{12}$ et $v_{23}$) l'essentiel véritable de cette loi est révélé: il parle de ce, laquelle vitesse relative des systèmes $S_3$ et $S_2$ l’observateur du système $S_1$ fixera, s’il utilise la règle de l’Einstein pour la synchronisation du temps (à l'aide de signaux lumineux) et la mesure des longeurs. En effet, de nouveau nous avons "la loi de l’apparence". (Cette expression sera changée pour le cas d’une dépendance paramètrique possible de la vitesse de lumière de la fréquence - regardez les Appendices).

Examinons une remarque méthodique suivante. Pour les notions cinématiques l’incommutativité de la loi de l’addition des vitesses pour les vecteurs qui ne sont pas parallèles est fort étrange. La propriété de l’incommutativité (et ce que les transformations de Lorentz sans rotation ne font pas une groupe) est légèrement mentionné seulement dans quelques manuels de la physique théorique. Cependant, par exemple dans la mécanique quantique la propriété analogue change considérablement tout appareil mathématique et physiquement exprime l’impossibilité simultanée de mesurer des grandeurs incommutables.

De la loi générale relativiste de l’addition des vitesses

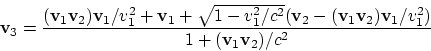$${\bf v}_3 = {({\bf v}_1{\bf v}_2){\bf v}_1/v_1^2 + {\bf v}_1... ...1{\bf v}_2){\bf v}_1/v_1^2)\over 1 + ({\bf v}_1{\bf v}_2)/c^2}$$ (1.6)

il est clair que le résultat dépend de l’ordre de la transformation: par exemple, dans le cas de la suite

$$+v_1{\bf i}, -v_1{\bf i}, +v_2{\bf j}, -v_2{\bf j},$$

où ${\bf i}$ et ${\bfj}$ - les vecteurs unitaires du système rectangulaire des coordonnées, on reçoit une vitesse finale zéro, mais pour un autre ordre de même grandeurs

$$+v_1{\bf i}, +v_2{\bf j}, -v_1{\bf i}, -v_2{\bf j}$$

on reçoit une vitesse pas zéro, qui dépend assez complexement de vitesses $v_1$ et $v_2$. L’application conséquente des transformations (des mouvements) $v_1{\bf i}$ et $v_2{\bf j}$ amène à

$${\bf v}_3 = v_1{\bf i} + \sqrt{1-v_1^2/c^2}v_2{\bf j},$$

mais dans un autre ordre $v_2{\bf j}$ et $v_1{\bf i}$ amène à

$${\bf v}'_3 = v_2{\bf j} + \sqrt{1-v_2^2/c^2}v_1{\bf i},$$

c’est-à-dire on reçoit les vecteurs différents (Figure 1.21).

Figure 1.21: Les parallélogrammes des vitesses dans la théorie de la relativité restreinte.

Qu’est-ce que dans ce cas la décomposition du vecteur de la vitesse en componants signifie? Premièrement, le transfert des méthodes classiques des calculs les plus simples (de l’algèbre commutative) aux équations relativistes (qui ne sont pas commutatives) est incorrect: même la solution des équations vectorielles par componant exige de postulats supplémentaires, de compliquations ou d’éclaircissements. Deuxièmement, l’application simple des méthodes de la physique classique (du principe de déplacements virtuels, de méthodes variantes etc.) est impossible. Il faudrait "individualiser" même le zéro: la quantité des grandeurs "zéro", faites d’une certaine combination vectorielle, doit être égale à la quantité des grandeurs "zéro", faites d’une combination vectorielle inverse. Par conséquent, même la théorie des fluctuations aurait besoin de la justification supplémentaire. Ainsi en dépit de la thèse "de la simplicité et de la beauté mathématique de la théorie de la relativité restreinte" pour la justification correcte même de procédures les plus simples il faudrait introduire la multitude de compliquations artificielles et d’éclaircissements (dont il n’y a pas dans les manuels).

Examinons la contradiction logique de la loi relativiste de l’addition des vitesses à l’exemple du cas unidimentionnel. Supposons que nous avons les balances, qui ont la forme d’une gouttière (chéneau) horizontale avec un axe transversal (horizontal) au milieu de la gouttière. Deux mêmes billes de la masse $m$ rouleront dans les côtés différents de l’axe (Figure 1.22).

Figure 1.22: La loi de l’addition des vitesses et la contradiction des balances.

Pour, pour l’instant, éviter la discussion des propriétés de la masse relativiste faisons comme ça. Supposons qu’on manque partout le frottement de l’axe des balances, excepté le point de la position horizontale ("le point mort"). Dans cette position le seuil de la force de frottement ne permet pas aux balances de se déplacer à cause d’une petite différence possible des masses relativistes (entre les billes), mais ce seuil de la sensibilité ne peut pas obstacler à la rotation des balances (du "point de mort") en cas de l’absence d’une bille (si elle tombe). Supposons que les vitesses des billes dans le système des balances sont égales en modulo. Alors dans ce système les billes en même temps rouleront jusqu’aux bords et tomberont en bas, de la manière que les balances resteront en position horizontale. Analysons maintenent le même mouvement dans le système, relativement auquel les balances se déplacent à la vitesse $V$. Supposons que seulement $V\rightarrow c$, et $v\ll v_s$, où $v_s$ - la vitesse du son en matériau du chéneau. Alors on peut considérer les balances comme absolument rigides (ignorer les vagues acoustiques). Selon la loi relativiste de l’addition des vitesses

$$v_1 = {V-v\over 1-vV/c^2}~, ~~~~~ v_2 = {V+v\over 1+vV/c^2}~.$$

Le mouvement du point moyen à la vitesse

$${v_1 + v_2\over 2} = V{1 - v^2/c^2\over 1 - v^2V^2/c^4} < V$$

reste toujours en arrière du mouvement des balances. Ainsi, la bille, se déplaçant contre la direction du mouvement des balances, tombera la première. En résultat, l’équilibre enfreindra et les balances commenceront de tourner. Nous avons l’incohérence avec les donnés du premier observateur. Qu’est-ce qui se passera avec l’observateur, s’il se trouve sous une partie droite des balances?

Les transformations de Lorentz, peuvent-elles décrire les passages consécutifs d’un système inertiel à un autre? Et la loi relativiste de l’addition des vitesses, répond - elle aux changements réels des vitesses? Bien sûr que non. D’abord rappelons lequel sens on met dans la loi relativiste de l’addition des vitesses. Il doit démontrer que l’addition des mouvements ne peut pas mener à la vitesse, plus grande que la vitesse de la lumière. Comment en ce cas là peut-on additionner les mouvements? Par exemple, notre Terre se déplace relativement aux étoiles (de fait il existe le premier système mouvant de référence), une fusée prend son vol de la Terre à une grande vitesse (de fait le deuxième système mouvant de référence est "cré"), après une autre fusée prend son vol de cette fusée (le troisime système de référence) etc. On doit supposer justement cela sous l’application conséquente des transformations. Alors, par exemple, la question de ce laquelle des vitesses on doit estimer la première et la deuxième (c’est important pour les transformations pas commutatives) disparaît. Tous les exemples au-dessus furent donnés en ce sens.

Examinons maintenent les transformations de Lorentz pour les directions arbitraires du mouvement

$${\bf r}_1 = {\bf r} + {1\over V^2}\biggl ( {1\over \sqrt{1-V... ...\biggr ) ({\bf rV}){\bf V} + {{\bf V}t\over \sqrt{1-V^2/c^2}},$$

$$t_1 = {t + ({\bf rV})/c^2\over \sqrt{1-V^2/c^2}}.$$

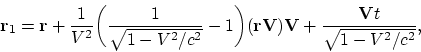
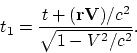
Il est facile de verifier, que l’application de la loi relativiste de l’addition des vitesses (1.6) pour les grandeurs

$$v_1{\bf i}, ~~ v_2{\bf j}, ~~ -v_1{\bf i} - v_2\sqrt{1-v_1^2/c^2}{\bf j}$$ (1.7)

mène au zero. Mettons conséquemment en application les transformations de Lorentz pour le vecteur arbitraire ${\bf r} = x{\bf i} + y{\bf j}$ avec la même composition des vitesses. Il en suit:

$${\bf r}_1 = {x+v_1t\over \sqrt{1-v_1^2/c^2}}{\bf i} + y{\bf j},$$

$$t_1 = {t+xv_1/c^2\over \sqrt{1-v_1^2/c^2}}.$$

Puis on a:

$${\bf r}_2 = {x+v_1t\over \sqrt{1-v_1^2/c^2}}{\bf i} + {y\sqr... ...xv_1v_2/c^2\over \sqrt{1-v_1^2/c^2}\sqrt{1-v_2^2/c^2}}{\bf j},$$

$$t_2 = {t+xv_1/c^2+yv_2\sqrt{1-v_1^2/c^2}/c^2\over \sqrt{1-v_1^2/c^2}\sqrt{1-v_2^2/c^2}}.$$

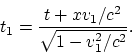
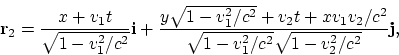
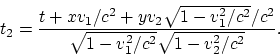
Nous ne citons pas les expressions pour ${\bf r}_3$ et $t_3$ en vue de leurs encombrement. Pourtant, utilisant les logiciels graphiques on peut s'assurer de propriétés suivantes:

1) dans un nouveau système le temps initial est désynchronisé dans n’importe quel point de l’espace, outre le début des coordonnées.

2) Les intervalles de temps changèrent: $dt_3\ne dt$, c’est à dire nous nous retrouvâmes dans un nouveau système en mouvement, mais pas dans un système initial en état de repos. C’est à dire, le sens des transformations de Lorentz ou de la loi relativiste de l’addition des vitesses n’est pas exactement révélé dans les manuels.

3) Les segments sont non seulement d’une longueur changée, mais ils sont tournées. Il est facile de s'en assurer si on va trouver numériquement l’angle de tournant, c’est à dire la différence

$$\alpha = \arctan\Biggl ( {y_3[x(1),y(1),t]-y_3[x(0),y(0),t]\over x_3[x(1),y(1),t]-x_3[x(0),y(0),t]}\Biggr ) -$$

$$- \arctan\Biggl ( {y(1)-y(0)\over x(1)-x(0)}\Biggr ) .$$

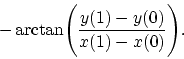
On peut sans fin expliquer mathématiquement ces propriétés par l’pseudoeuclidité de le métrique, mais physiquement tout est simple. Ces propriétés démontrent le caractère pas objectif (mais apparent) des transformations de Lorentz et de la loi de l’addition des vitesses et leur désaccord entre eux mêmes. Réellement, comme on passait conséquentement d’un système inertiel à un autre, et le tournant signifiait l’absence de l’inertialité du système, alors la théorie de la relativité restreinte elle même passent les limites de sa propre application, c’est à dire elle est contradictoire. Si ce tournant était réel, cela signifierait la subjectivité de la notion du système inertiel (comme le résultat dépenderait du moyen de passage à ce système) et, comme conséquence, l’absence de la base pour l’existence de la théorie de la relativité restreinte.

Esseyons de comprendre, pourquoi les manières de traiter de manuels mènent au désaccord de deux expressions: de la loi de l’addition des vitesses et des transformations de Lorentz, malgré ce que la première expression est tirée de la deuxième. Rappelons ce déduction à l’exemple du mouvement réciproque à une mesure des systèmes $K$ et $K'$. De transformations de Lorentz

$$x_1 = {x+Vt\over \sqrt{1-V^2/c^2}}~, ~~~~ t_1 = {t+Vx/c^2\over \sqrt{1-V^2/c^2}}$$

on divise la différentielle $dx_1$ en $dt_1$ à compte des definition $v=dx/dt$ et $v_1=dx_1/dt_1$ et on reçoit:

$$v_1 = {v+V\over 1+vV/c^2}.$$

De cela on voit que:

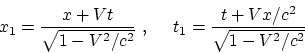
1) l’observateur se trouve au centre du système $K$ et mesure la distance $x$ jusqu’au corps étudié dans son système $K$.

2) il compte que le temps $t$ est unique dans son système et détermine la vitesse du corps dans son système $v=dx/dt$.

3) il mesure la vitesse $-V$ du système $K'$ relativement au $K$, utilisant son propre (!) temps, et estime que les vitesses relatives de systèmes sont de retour réciproques en direction. L’observateur ne peut pas mesurer rien d’autre: la grandeur résultative de la vitesse $v_1$ est une grandeur calculable. Comme ça on arrive à la manière de traiter [49], exposée au dessus: la loi relativiste de l’addition des vitesses détermine la vitesse du tel mouvement relatif, auquel l’observateur lui même ne participe pas. Cet effet n’est pas réel, mais apparent (quand on utilise les règles déterminées de la théorie de la relativité restreinte). En fond de la formule nous ne pouvons pas tout simplement passer à la deuxième substitution pour la détermination $v_2$, bien que formalement on peut substituer successivement n’importe quel nombre des grandeurs à l’expression de la loi relativiste de l’addtion des vitesses. En cas de l’addition des mouvements le loin d’une droite la propriété classique de la commutatibilité se conserve et la contradiction se trouve voilée. Mais si les vecteurs de la vitesse ne sont pas parallèles, le point 3) se trouve injuste et la contradiction et le désaccord de la loi de l’addition des vitesses et des transformations de Lorentz se démontrent tout de suite.

Dans l’exemple examiné au dessus on peut agir à une autre manière: cherchons la conséquence de trois transformations des vitesses, qui garde le temps initial dans les transformation de Lorentz immuable. Alors il est facile de vérifier, qu’au lieu de (1.7) la conséquence unique peut être prise:

$$v_1{\bf i}, ~~ v_2{\bf j}, ~~ -v_1\sqrt{1-v_2^2/c^2}{\bf i} - v_2{\bf j} .$$ (1.8)

Cependant, premièrement le tournant des segments reste. Deuxièmement une nouvelle composition des vitesses ne correspond pas dans cette consequence à la loi de l’addition des vitesses, c’est à dire qu’en fait l’ordre de la substituation des vitesses $v_1$ et $v_2$ dans la loi de l’addition des vitesses changea (ce que ne correspond pas à l'essence de cette loi). Ainsi, les contradictions ne s’éliminent pas tout de même. L’une des preuves de la contradiction de la théorie de la relativité restreinte est la précession de Tomas: en partant de la conséquence des systèmes inertiels (qui se déplacent tout droit et régulièrement) soudant en résultat on reçoit la rotation de l’objet (le mouvement pas inertiel de principe). Ainsi, le passage de transformations de Lorentz dans "l’espace mathématique" 1+1 ($t+x$) exposées dans les manuels standards vers les transformation de Lorentz dans "l’espace" 1+2 ou 1+3 contient les contradictions physiques.

Beaucoup de propriétés de grandeurs physiques compréhensibles par intuition perdent leur sens dans la théorie de la relativité restreinte. Par exemple, la vitesse relative cesse d’être invariante. Les particules partant le long d’une droite aux vitesses différentes forment dans la théorie de la relativité restreinte "un éventail composé des vitesses" pour un système en mouvement. La distribution isotrope sur les vitesses dans la théorie de la relativité restreinte n’existe pas pour un autre sistème en mouvement. Il n’y a pas aucune simplification déclarée dans la théorie de la relativité restreinte.

De la théorie de la relativité restreinte ne suit pas du tout l’impossibilité des vitesses $v > c$. Et l’addition que cela se rapporte seulement à la vitesse de la transmission du signal - est une addition factice (en vue de la présence des contre-exemples évidents pour l’interprétation élargie). Cependant même avec une addition pareille la notion du signal (de l’information) reste assez indéterminée. Par exemple, reçevant le signal d’un éclat de supernova, est-ce que nous ne sommes pas sûrs que la même information est "contenue" à une distance diamétralement opposée de la supernova, alors nous savons cela à la vitesse $2c$? Ou ce n’est pas une information? Par conséquent, dans la théorie de la relativité restreinte on peut parler seulement de l’information sur un porteur matériel de la nature électromagnétique, qui se répand dans le vide successivement à travers tous les points de l’espace de la source jusqu’au récepteur du signal.

Faisons une remarque au sujet de "l’étonnance" de la loi relativiste de "l’addition" des vitesses, qui permet d’échanger du signal de lumière même quand une somme algébrique des vitesses est plus grande que $c$. Remarquons un fait évident: les signaux pour l’echange de l’information doivent être envoyés sans faute dans la direction de l’objet, mais pas dans une direction opposée. C'est pourquoi il n'a rien d'étonnant en échange des signaux, quand même dans le cas classique en résultat de l’addition formelle des vitesses on a $v_1+v_2>v_{signaux}$. Supposons que deux avions décollent de l’aérodrome $O$ aux vitesses $0.9v_{son}$ et s’envolent l’un de l’autre en dirrections opposées de l’axe $X$ (c’est à dire à une vitesse relative $1.8v_{son}$). Est-ce que l’échange des signaux sonores est possible entre eux? Bien sûr! Comme une onde sonore se propage dans l’air indépendamment de la vitesse de la source $S_1$ au moment d’émission d’un signal, le premier avion (qui émit le signale) rejoindra le front de l’onde, se répandant en direction positive de l’axe $X$, le deuxième avion "rivalisera" avec le front de l’onde, se répandant en direction négative de l’axe $X$. Les deux avions se déplacent plus lentement, que les parcelles correspondantes du front de l’onde les plus proches à eux (Figure 1.23).

Figure 1.23: L’echange d’un signal.

Ainsi, la somme des vitesses en réalité est confrontée (par une manière difficile) pas à une vitesse de son, mais à une grandeur $2v_{son}$ (pour la lumière - à une grandeur $2c$).

Il est aussi évident, qu’une limitation phisique à la grandeur de la vitesse ne peut pas être mise par les mathématiques (le fait qu’une valeur négative sera mise sous le signe du radical dans quelques expressions). Il faut tout simplement se souvenir de ce que toutes les formules de la théorie de la relativité restreinte sont reçues à l’utilisation de l’echange des signaux de lumière (la méthode de la synchronisation d’Einstein). Mais si le corps se déplace tout de suite plus vite que la lumière, alors il ne pourra pas rattraper le signal, envoyé à sa poursuite. Par analogie on peut introduire la synchronisation à l’aide d’un son (et aussi on aura les singularités dans les formules), mais l’impossibilité des vitesses supersoniques ne s'en suvra. La vitesse de la propagation des indignations (sonores ou lumineuses) dans le milieu n’est absolument pas liée avec la vitesse du mouvement d’un corps à travers ce milieu.