La geometría del espacio

La cuestión en la TGR sobre la posibilidad de cambiar la geometría del espacio es completamente incorrecta. El carácter finito de la velocidad de transmisión de las interacciones puede cambiar sólo las leyes físicas y no las matemáticas. Claro que no afirmaremos que no existe la recta, ya que para su trazado hasta el infinito se requiere, incluso a la velocidad de la luz, un tiempo infinito (de forma análoga para el plano y el espacio). El sentido matemático de las derivadas tampoco puede intercambiarse. Una de las demostraciones de la TGR "sobre el cambio ineludible de la geometría en un sistema no inercial" consiste en lo siguiente: en un sistema de referencia que guira la relación de la longitud de la circunferencia con respecto a su diámetro será, a causa de la contracción de las longitudes, menor que $\pi$. Notemos que nadie pudo dibujar una "nueva geometría" para este caso: no se puede representar lo que no existe. En realidad no cambiará no sólo la geometría real, sino tampoco lo hará la geometría observable: no se moverá o cambiará una línea matemática al movernos. Aunque en la teoría de la relatividad el radio, que es perpendicular al movimiento de la circunferencia, no deberá cambiar, supongamos inicialmente que la circunferencia se moverá radialmente. Sea que tenemos tres circunferencias concéntricas de radios casi iguales (Fig. 2.1).

Figura 2.1: Geometría de la circunferencia giratoria.

Coloquemos observadores en ellas y numerémoslos en orden a partir del centro: 1, 2, 3. Supongamos que el segundo observador estará inmóvil y que el primero y el tercero giran alrededor del centro O en dirección y contra la dirección de las agujas del reloj a una velocidad angular igual. Entonces, a consecuencia de la diferencia de las velocidades relativas y de la contracción de las longitudes, los observadores intercambiarán lugares. Empero, cuando resulten estar en un mismo punto del espacio, ellos verán cuadros diferentes. Efectivamente, el primer observador verá la siguiente disposición a partir del centro: 3, 2, 1, mientras que el segundo observador verá un orden diferente: 1, 3, 2, y sólo el tercer observador verá el cuadro inicial: 1, 2, 3. Tenemos una contradicción. Supongamos ahora que cambió la geometría del plano en rotación. ¿Pero que es entonces preferible: arriba o abajo? El problema es simétrico ¿hacia donde se alargó, pues, el plano? Si hacemos la última suposición de que el radio se curvó (como cambia el movimiento aparente en un sistema no inercial), entonces el segundo observador lo verá no curvado, y el primero y el tercero considerarán que está "curvado" hacia diferentes lados. De este modo, tres observadores ven en un mismo punto para un mismo espacio panoramas diferentes. Por consiguiente, la curvatura no es objetiva (y no puede ser objeto de estudio científico).

La circunferencia en rotación demuestra la contradicción de las ideas de la TER y de la TGR. Efectivamente, de acuerdo a los libros de texto, el radio perpendicular al movimiento no cambia. Por lo tanto, las circunferencias permanecerán en sus lugares independientemente del movimiento. Coloquemos en una circunferencia en reposo a observadores equidistantes y emitamos un destello puntual desde el centro de la circunferencia para que los observadores marquen rayas sobre la circunferencia en movimiento en el momento en que les llegue la señal (Fig. 2.2).

Figura 2.2: Observadores equidistantes sobre una circunferencia.

A consecuencia de la simetría del problema, las rayas también serán equidistantes. Durante los sucesivos destellos periódicos cada observador reafirmará que en el momento del destello pasa delante de el la marca trazada (con la frecuencia correspondiente de los destellos), o sea que las longitudes de los segmentos de las dos circunferencias, la que está en movimiento y la que está en reposo, son iguales. Al detener la circunferencia las marcas permanecerán en su lugar. El número de marcas equidistantes (que es igual al número de observadores) no cambiará. Luego, en el caso inmóvil las longitudes de los segmentos también son iguales. De esta manera no hubo en absoluto ninguna contracción de las longitudes (ni un cambio en la geometría).

Veamos nuevamente la cuestión sobre la geometría del espacio pero desde otro punto de vista. Esta pregunta ha estado completamente enredada ya desde los tiempos de Gauss, el cual quizo determinar la geometría con ayuda de los rayos de luz. Las limitacines de uno u otro experimento no pueden influir en los conceptos matemáticos ideales. Notemos que la luz en la TGR se mueve incluso no por la línea más corta: en la TGR en lugar del principio de Fermat $\delta\int dl=0$ tenemos [17]: $\delta\int (1/\sqrt{g_{00}})dl=0$, donde $g_{\alpha\beta}$ es un tensor métrico. ¿Que es entonces lo que destaca a la luz? En los libros de texto frecuentemente se "fundamenta" la necesidad del cambio de la geometría de esta manera: para que la luz dibuje un triángulo cerrado en el campo gravitacional, los espejos deberán estar girados un cierto ángulo; como resultado, la suma de los ángulos del triángulo será diferente de $\pi$. No obstante, para cualquier cuerpo puntual y tres espejos, en el campo de la gravedad (ver la Fig. 2.3) se puede escribir la suma de los "ángulos":

$$\sum\beta_i = \pi + 4\arctan{\Biggl ( {gL\over 2v_0^2}\Biggr ) } - 2\arctan{\Biggl ( {gL\over v_0^2}\Biggr ) }.$$

Figura 2.3: "La geometría del triángulo".

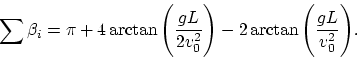
Resulta que la geometría de un mismo espacio depende de las condiciones del experimento: de $L$ y $v_0$. Puesto que el ángulo $\alpha$ entre los expejos $A$ y $B$ también se puede cambiar (en nuestro dibujo él es nulo $\alpha =0$), obtenemos la posibilidad de un cambio artificial de la geometría dentro de unos límites bastante amplios. Notemos que los parámetros variables (de $L$ y $\alpha$) permanecen también para la luz. En tales demostraciones "verosímiles" sobre la necesidad de cambiar la geometría no se acentúan ciertos momentos. En primer lugar, tanto en los experimentos con puntos materiales como con la luz la geometría se "dibuja" no inmediatamente, sino paulatinamente en el transcurso de un cierto tiempo. En segundo lugar, para los sistemas acelerados las partículas (y la luz) se mueven en el vacío de forma rectilínea según la ley de la inercia y, prácticamente, a este movimiento se agrega aditivamente el movimiento de los límites de dicho sistema acelerado. Todos los ángulos de incidencia (en el sistema de laboratorio) son iguales a los correspondientes ángulos de reflexión y la "geometría de los ángulos" no cambia en absoluto. Simplemente la figura resulta abierta a acusa del movimiento de los límites. En tercer lugar, el papel de límites no se descubre en absoluto al determinar las relaciones entre las longitudes de los cuerpos reales. Por ejemplo, si todos los puntos de un cuerpo real están sometidos a la acción de una misma fuerza aceleradora, entonces la relación mutua de las longitudes y los ángulos ("la geometría") permanece igual. Si a la aceleración están sometidos solamente los límites, entonces todos los cambios reales en las dimenciones de los cuerpos ocurren sólo durante la interacción con los límites. En cualquier caso se pueden trazar líneas rectas euclidianas. Por ejemplo, tomemos dos varillas largas iguales para trazar una línea horizontal en un campo gravitacional (Fig. 2.4).

Figura 2.4: El trazado de una recta en el campo gravitacional.

Coloquemos el apoyo puntual de la primera varilla a la mitad de ésta. Como resultado de la flexión de la varilla se forma una línea convexa hacia arriba. Los dos apoyos puntuales para la segunda varilla los pondremos en los extremos caidos de la primera varilla. Como resultado de la flexión de la segunda varilla se formará una línea convexa hacia abajo. La línea media entre estas dos varillas flexionadas determina la línea recta.