Теория столкновений и законы сохранения в СТО

Очень часто в СТО для "упрощения" описания столкновений используют прием перехода в какую-нибудь "удобно движущуюся" систему отсчета. Однако, такая процедура не имеет под собой никаких физических оснований и принцип относительности для закрытых идентичных систем здесь вовсе ни при чем. Если проводятся релятивистские эксперименты на искусственных пучках частиц, то источники (ускорители) и регистрирующие приборы привязаны к Земле и от нашего мысленного представления ускорители и приборы не полетят с движущимся наблюдателем. Если изучается некоторый процесс в камере Вильсона, то треки частиц привязаны к среде (то есть к камере Вильсона), а не к летящему наблюдателю. Например, в классической физике угол между треками частиц не изменится от движения наблюдателя. В то же время угол между скоростями частиц, оставляющих указанные треки, может зависеть от скорости движения наблюдателя. В релятивистской физике углы между траекториями и между скоростями частиц тоже зависят по разным законам от скорости движения наблюдателя. Поэтому такой казалось бы правдоподобный с точки зрения СТО переход к новой системе отсчета может существенно исказить интерпретацию решения, то есть любой процесс должен рассматриваться только в системе реального наблюдателя (регистрирующего прибора).

Еще одним искажением действительности является рассмотрение процесса столкновения двух частиц (принципиально точечных в СТО) как плоского движения. На самом деле даже при исследовании статистических характеристик точечных частиц измерительный прибор не может (для подгонки под идеальную задачу движения двух точек) с каждой парой частиц лететь и вращаться по-своему (по-разному!) - положение прибора фиксировано. Кроме того точечные частицы должны рассматриваться как предельный случай частиц реального конечного размера, иначе не наблюдалось бы лобовых столкновений, нельзя было бы рассматривать столкновения атомов и молекул, протоны не имели бы структуры и т.д.. А в этом случае столкновение частиц является принципиально трехмерным (вероятность плоского движения равна нулю). Пусть, например, два одинаковых шарика (1 и 2) приближаются друг к другу до столкновения по скрещивающимся в пространстве прямым (минимальное расстояние между прямыми меньше диаметра шарика). Уже с самого начала эксперимента мы не можем провести через эти заданные прямые плоскость. Тем не менее, возьмем середину минимального расстояния между скрещивающимися прямыми (траекториями до столкновения) и проведем через нее пересекающиеся прямые, параллельные данным траекториям.

Рисунок 4.8: Неплоское движение двух частиц.

Теперь через пересекающиеся прямые проходит единственная плоскость $\alpha$ (Рис. 4.8). Центры шариков движутся до столкновения параллельно этой плоскости: центр первого шарика движется чуть выше плоскости, а центр второго шарика - чуть ниже этой плоскости. После столкновения шарики полетят по другим скрещивающимся прямым. Опять нельзя через эти прямые провести плоскость. Снова проделаем аналогичную процедуру с параллельным переносом прямых, на которых лежат линии движения после столкновения, до пересечения посредине. Проведем через пересекающиеся прямые плоскость $\beta$ (опять центры шариков будут двигаться по разные стороны от этой плоскости). Однако, "плоскость до столкновения" не совпадает с "плоскостью после столкновения", а пересекает ее под некоторым углом.

Второй способ: проведем одну плоскость $\gamma$ через траекторию движения первой частицы (пересекающиеся прямые ее движения до и после столкновения), а вторую плоскость $\delta$ - через аналогичную траекторию движения второй частицы. Однако, эти плоскости тоже пересекаются под некоторым углом (Рис. 4.9).

Рисунок 4.9: Трехмерность столкновения двух частиц.

Что же следует из трехмерности движения? Первое. Не все связи оказываются линейными. Например, даже при прямолинейном равномерном движении тел по скрещивающимся прямым, расстояние между телами оказывается нелинейной функцией времени. Второе. Запишем классические законы сохранения импульса (в проекциях) и энергии:

$$v_{1x} + v_{2x} = v'_{1x} + v'_{2x}$$ (4.3)

$$v_{1y} + v_{2y} = v'_{1y} + v'_{2y}$$ (4.4)

$$v_{1z} + v_{2z} = v'_{1z} + v'_{2z}$$ (4.5)

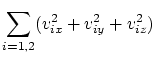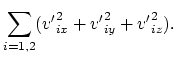$$\sum_{i=1,2}(v^2_{ix} + v^2_{iy} + v^2_{iz}) = \sum_{i=1,2}({v'}^2_{ix} + {v'}^2_{iy} + {v'}^2_{iz}).$$ (4.6)

Из системы (4.3-4.6) мы видим, что для шести неизвестных величин ($v'_{1x}, v'_{1y}, v'_{1z}, v'_{2x}, v'_{2y}, v'_{2z}$) имеются всего четыре уравнения. Таким образом, должно остаться два неопределенных параметра в решении. Если же считать движение плоским (убрать уравнение (4.5)), то для оставшихся четырех неизвестных будем иметь три уравнения. Следовательно, при сопоставлении решений СТО с классической физикой осуществляется подмена решений и остается только один неопределенный параметр (обычно таковым считают угол рассеяния). Такая подмена приводит к неправильной интерпретации данных эксперимента, особенно при восстановлении недостающих величин. Например, в книге [33] демонстрируются два трека разлета частиц одинаковой массы и заряда (точнее одинакового отношения $e/m$?) с углом разлета меньшим $90^{\circ}$ и отсюда делается вывод о неверности классической механики. Запишем выражение для угла $\alpha$ между траекториями разлетающихся частиц:

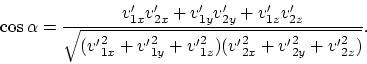$$\cos\alpha = {v'_{1x}v'_{2x} + v'_{1y}v'_{2y} + v'_{1z}v'_{2... ...1y} + {v'}^2_{1z})({v'}^2_{2x} + {v'}^2_{2y} + {v'}^2_{2z})}}.$$ (4.7)

Выберем ось $Z$ так, чтобы было $v_{1z}=v_{2z}=0$. Выразим теперь переменную $v'_{1x}$ из уравнения (4.3), переменную $v'_{1y}$ выразим из уравнения (4.4), переменную $v'_{1z}$ выразим из уравнения (4.5), а из уравнения (4.6) выразим величину ${v'}^2_{2z}$ (при этом условие ${v'}^2_{2z}>0$ ограничивает область возможных значений всех переменных). Подставим все вышеназванные величины в уравнение (4.7). В результате получится двухпараметрическая зависимость от $v'_{2x}$ и $v'_{2y}$, которую мы не выписываем вследствие ее громоздкости. Используя графические программы, можно убедиться, что при заданных величинах $v_{1x}, v_{1y}, v_{2x}, v_{2y}$ получается некоторая поверхность, похожая на внутреннюю часть цилиндра, то есть величина $\cos\alpha$ меняется в широких пределах. Например, легко проверить, что значения

$$v_{1x}=0,1; ~ ~ ~ v_{1y}=0,1; ~ ~ ~ v_{2x}=0,7; ~ ~ ~ v_{2y}=0,7; ~ ~ ~ v'_{1x}=0,6;$$

$$v'_{2x}=0,2; ~ ~ ~ v'_{1y}=0,4; ~ ~ ~ v'_{2y}=0,4; ~ ~ ~ -v'_{2z}=v'_{1z}=\sqrt{0,14}$$

удовлетворяют всем классическим законам сохранения (4.3-4.6). Для этих значений получаем $\cos\alpha = 0,29554$, то есть $\alpha\approx 72,8^{\circ}$. Заметим: если считать скорости выраженными в единицах скорости света, то меньшая скорость вполне реальна для движения внутренних электронов в атомах, начиная с $z\ge 60$. Да и в общем случае никто не видел покоящихся электронов в атомах! Угол в $90^{\circ}$ однозначно получается в классической физике при столкновении с покоящейся частицей в системе регистрирующего прибора (только где найти такую частицу?). Однако, из наблюдаемого угла разлета в $90^{\circ}$ вовсе не следует с однозначностью обратное утверждение о том, что одна из частиц покоилась (математическая вероятность такого события бесконечно мала). Таким образом, обратная задача восстановления недостающих данных не является однозначной процедурой ни в классической, ни в релятивистской физике (существует бесконечное число различных непротиворечивых решений).

Для более строгой экспериментальной проверки законов сохранения при столкновениях (независимо от теории) необходимо изучать столкновения частиц в вакууме для узких моноэнергетических пучков известных частиц при заданных углах столкновения. При этом полное исследование процесса столкновения должно включать в себя проверку баланса по энергиям частиц (для каждого угла рассеяния в пространстве), проверку баланса импульсов частиц, проверку баланса общего количества частиц в пучках до и после столкновения (вероятность рассеяния), проверку баланса возникающего излучения по энергиям и направлениям. Есть еще два вопроса, на которых обычно не акцентируется внимание (еще две неопределенности): зависит ли рассеяние от взаимной ориентации собственных моментов вращения сталкивающихся частиц? И меняются ли собственные моменты вращения в процессе столкновения? В классической физике ответ на эти вопросы утвердителен (но в количественном плане сильно зависит от "устройства" шариков).

Автор не встречал полного анализа какого-либо процесса столкновения в СТО согласно всем вышеперечисленным пунктам. Отсюда не следует однозначного вывода о неверности (в пределах экспериментальных ошибок) обычно используемых релятивистских законов сохранения в любом процессе столкновения (хотя для многих отдельных случаев это вполне может оказаться так). Автор только утверждает, что не существует даже отдельных примеров абсолютного подтверждения релятивистских законов столкновения (не говоря уже о рекламируемой глобальной подтверждаемости).

С принципиально строгих позиций применение релятивистских законов сохранения к процессу столкновения в физике элементарных частиц весьма сомнительно. Могут ли они сохранять свой вид независимо от заряда сталкивающихся частиц, углов столкновения и углов разлета? Ведь в процессе столкновения заряженные частицы испытывают ускорение. Следовательно, согласно современным представлениям (в том числе в СТО) всегда должно наблюдаться некоторое излучение (поле). Неужели нужно действовать как студенты, подсматривающие в ответ задачи: если уж прибор зарегистрировал $\gamma$-квант ("поймал нас за руку"), то его нужно явно учесть "с умным видом". А в остальных случаях "с умным видом" верить в правильность формул СТО? Где же "предсказательная сила" СТО? На самом деле в законы сохранения нужно явно добавить члены, учитывающие энергию и импульс поля.

Вообще говоря, единственный случай, когда правомерно обсуждение релятивистских законов сохранения при "столкновениях" - это взаимодействие частиц силами электромагнитной природы (силой Лоренца). Для остальных случаев выполнение релятивистских законов сохранения - это непроверенная гипотеза (световые сферы СТО не имеют никакого отношения к силам неэлектромагнитной природы). Однако, и в случае электромагнитных взаимодействий для вывода релятивистских законов сохранения вовсе не требуется никаких идей СТО. Известно, что уравнения движения с начальными условиями полностью определяют все характеристики движения, в том числе интегралы движения. Таким интегралом движения может быть энергия (но не всегда). Из уравнения движения следует

$${d{\bf P}\over dt} = {\bf F} ~ ~ \Rightarrow ~ ~ {\bf v}d{\bf P} = {\bf F}d{\bf r}.$$ (4.8)

Вводим определение потенциальной энергии

$$U = - \int_{r_0}^r {\bf F}d{\bf r}.$$

Зная вид импульса (это величина, входящая в экспериментальное уравнение движения (4.8)), например, в классическом случае

$${\bf P} = m{\bf v}$$

а в релятивистском случае

$${\bf P} = m{\bf v}/\sqrt{1-v^2/c^2},$$

можно получить закон сохранения энергии из

$$dE={\bf v}d{\bf P} - {\bf F}d{\bf r}$$

- соответственно классический

$$U+mv^2/2=constant$$

или релятивистский

$$U+mc^2/\sqrt{1-v^2/c^2}=constant.$$

При условии равенства сил действия и противодействия (третий закон Ньютона, гипотеза центральных сил) имеем: ${\bf F}_{12}=-{\bf F}_{21}$. Тогда из уравнения движения (4.8) можно получить закон сохранения импульса (опять это величина, входящая в экспериментальное уравнение движения (4.8)): из $d{\bf P_1}/dt={\bf F}_{12},~ ~ d{\bf P_2}/dt={\bf F}_{21}$ получаем

$${d({\bf P}_1+{\bf P}_2)\over dt} = 0, ~ ~ \Rightarrow ~ ~ {\bf P}_1+{\bf P}_2=const.$$

Однако, при наличии магнитных сил ${\bf F}_{12}\ne -{\bf F}_{21}$ и релятивистский закон сохранения импульса частиц в общем случае может нарушаться. Поскольку большинство частиц, даже многие электрически нейтральные, имеют магнитный момент (то есть представляют собой не "идеальные точечные заряды СТО", а заряженные магнитные ротаторы конечных размеров), то применение релятивистского закона сохранения импульса в ядерной физике и физике элементарных частиц без явного учета импульса поля совершенно неправомерно. Следовательно, мы опять приходим к необходимости явного учета импульса поля, а значит и его энергии, при столкновениях. (Возможно, это поможет упорядочить ядерную физику и физику элементарных частиц и сократить число частиц-призраков?)

Учет силы реакции излучения также ведет к нарушению заявленных в СТО законов сохранения энергии и импульса. Отказаться от учета этой силы в процессе столкновения частиц? Так ведь там эта сила и должна быть наиболее существенной (имеются большие поля вследствие сближения высокоэнергетических частиц и большие переменные ускорения).