Геометрия пространства

Вопрос о возможности изменении геометрии пространства в ОТО совершенно некорректен. Конечность скорости передачи взаимодействий может поменять только физические, а не математические законы. Не будем же мы утверждать, что прямая не существует, так как для ее проведения в бесконечность даже со скоростью света потребуется бесконечное время (аналогично для плоскости и пространства). Математический смысл производных тоже не может поменяться. Одна из демонстраций ОТО "о неизбежности изменения геометрии в неинерциальной системе" состоит в следующем: во вращающейся системе отсчета, вследствие сокращения длин, отношение длины окружности к ее диаметру будет меньше $\pi$. Заметим, что никто не смог нарисовать для данного случая "новую геометрию": невозможно изобразить несуществующее. На самом деле не поменяется не только истинная, но даже наблюдаемая геометрия: не будет же математическая линия передвигаться или меняться при нашем движении. Хотя в теории относительности радиус, перпендикулярный движению окружности, меняться не должен, тем не менее предположим вначале, что окружность будет двигаться радиально. Пусть имеем три концентрических окружности почти одинакового радиуса (Рис. 2.1).

Рисунок 2.1: Геометрия вращающейся окружности.

Поместим на них наблюдателей и пронумеруем их по порядку от центра: 1, 2, 3. Пусть второй наблюдатель будет неподвижен, а 1-й и 3-й вращаются вокруг центра $O$ по и против часовой стрелки с одинаковой угловой скоростью. Тогда, вследствие различия относительных скоростей и сокращения длин наблюдатели поменяются местами. Однако, когда они окажутся в одной точке пространства они увидят разную картину. Действительно, 1-й наблюдатель увидит следующее расположение от центра: 3, 2, 1, в то время как 2-й наблюдатель увидит иной порядок: 1, 3, 2, и только 3-й наблюдатель увидит первоначальную картину: 1, 2, 3. Имеем противоречие. Предположим теперь, что изменилась геометрия вращающейся плоскости. Однако, что тогда предпочтительнее: верх или низ? Задача ведь симметрична, куда же выгнулась плоскость? Если сделать последнее предположение, что искривился радиус (как меняется видимое движение в неинерциальной системе), то 2-й наблюдатель увидит его неискривленным, а 1-й и 3-й будут считать его "искривленным" в разные стороны. Таким образом, три наблюдателя видят в одной и той же точке для одного и того же пространства разную картину, следовательно искривление не объективно (и не может быть объектом научного изучения).

Вращающаяся окружность доказывает противоречивость идей СТО и ОТО. Действительно, согласно учебникам, перпендикулярный движению радиус не изменяется. Следовательно, окружности останутся на своих местах независимо от движения. Посадим на неподвижной окружности эквидистантно наблюдателей и дадим точечную вспышку из центра окружности, чтобы наблюдатели нанесли штрихи на движущуюся окружность в момент прихода сигнала (Рис. 2.2).

Рисунок 2.2: Эквидистантные наблюдатели на окружности.

Вследствие симметрии задачи, штрихи также будут эквидистантными. При последующих периодических вспышках каждый наблюдатель подтвердит, что в момент вспышки мимо него проходит штриховая метка (при соответствующей периодичности вспышек), то есть длины участков неподвижной и вращающихся окружностей равны. При остановке окружности метки останутся на своем месте. Число эквидистантных меток (равное числу наблюдателей) не изменится. Следовательно, в неподвижном случае длины участков также равны. Таким образом, никакого сокращения длин (и изменения геометрии) не было вовсе.

Рассмотрим опять вопрос о геометрии пространства, но с другой стороны. Этот вопрос совершенно запутан еще со времен Гаусса, который хотел определять геометрию с помощью световых лучей. Не может же ограниченность того или иного опыта влиять на идеальные математические понятия. Заметим, что свет в ОТО движется даже не по кратчайшей линии: вместо принципа Ферма $\delta\int dl = 0$ в ОТО имеем [17]: $\delta\int {(1/\sqrt{g_{00}})dl} = 0$, где $g_{\alpha\beta}$ - метрический тензор. Чем же в таком случае выделен свет? Часто в учебниках "обосновывается" необходимость изменения геометрии следующим образом: чтобы свет вычертил замкнутый треугольник в гравитационном поле, зеркала должны быть повернуты на некоторый угол, в результате сумма углов треугольника будет отличаться от $\pi$. Однако, для любого точечного тела и 3-х отражателей в поле тяжести (см. Рис. 2.3) можно записать сумму "углов":

$$\sum\beta_i = \pi + 4\arctan{\Biggl ( {gL\over 2v_0^2}\Biggr ) } - 2\arctan{\Biggl ( {gL\over v_0^2}\Biggr ) }.$$

Рисунок 2.3: "Геометрия треугольника".

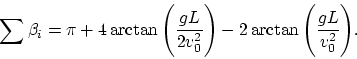
Получается, что геометрия одного и того же пространства зависит от условий опыта: от $L$ и $v_0$. Поскольку угол $\alpha$ между зеркалами $A$ и $B$ также можно менять (на нашем рисунке он нулевой $\alpha=0$), получаем возможность искусственного изменения геометрии в широких пределах. Заметим, что переменные параметры $\alpha$ и $L$ остаются и для света. В подобных "правдоподобных" доказательствах о необходимости изменения геометрии не подчеркиваются некоторые моменты. Во-первых, как в опыте с материальными точками, так и со светом геометрия "вычерчивается" не мгновенно, а последовательно в течение некоторого времени. Во-вторых, для ускоренных систем частицы (и свет) движутся в вакууме прямолинейно по закону инерции и, фактически, на это движение аддитивно накладывается движение границ этой ускоренной системы. Все углы падения (в лабораторной системе) равны соответствующим углам отражения и "геометрия углов" не меняется совершенно. Просто фигура получается незамкнутой за счет движения границ. В-третьих, роль границ совершенно не раскрывается при определении соотношений между длинами реальных тел. Например, если все точки реального тела подвержены действию одинаковой ускоряющей силы, то взаимное соотношение длин и углов ("геометрия") остается неизменным. Если же ускорению подвержены только границы, то все реальные изменения размеров тел происходят только при взаимодействии с границами. В любом случае можно провести Евклидовы прямые линии. Например, для проведения горизонтальной прямой в гравитационном поле возьмем два одинаковых длинных стержня (Рис. 2.4).

Рисунок 2.4: Проведение прямой в поле тяжести.

Точечную опору для первого стержня установим посредине стержня. В результате прогиба стержня образуется выпуклая вверх линия. Две точечные опоры для второго стержня установим на уровне двух опустившихся концов первого стержня. В результате прогиба второго стержня образуется выпуклая вниз линия. Средняя линия между этими двумя выгнувшимися стержнями определяет прямую линию.