The Mach principle

The Mach principle of stipulation of an inert mass and absolute nature of the acceleration due to the influence of far stars is also doubtful, since it explains the intrinsic properties of one body via the properties of other bodies. Of course, the idea is elegant in itself. If everything in the world is supposed to be interdependent and some ideal complete equation of state is believed to exist, then any property of bodies should be determined by the influence of the whole remaining Universe. However, in such a case any particle should be considered to be individual. This way is faulty for science, which progresses from smaller knowledge to greater, since "it is impossible to grasp the immense". Actually, if we take into account the non-uniform distribution of mass (in compact objects) and different values of attraction forces from close and far objects, then the complete "tugging" would be obtained instead of uniform rotation or uniform inertial motion of an object.

The Mach principle cannot be verified in essence: both removal of all bodies from the Universe and mathematical tending of the gravitation constant to zero are the abstractions having nothing in common with the reality. However, it is possible to estimate the influence of "far stars" experimentally by considering the mass of the Universe as mainly concentrated in compact objects. The force of attraction of a star having a mass of the order of the Sun's mass $M\sim 2\cdot 10^{30}$ kg, being at the distance of 1 light year $\sim 9\cdot 10^{15}$ m, is equivalent to the action of a load having a mass of only $m_0\sim 25 g$ at the distance of 1 meter. We shall make use, for a while, of the doubtful Big Bang theory and shall consider the time for the Universe to be equal to $\sim 2\cdot 10^{10}$ years. Even if the stars fly away with light speed, we would have the size of the Universe equal to $\sim 2\cdot 10^{10}$ light years. We will suppose the mean distance between nearest stars in 1 light year. We have deliberately increased all quantities; for example, the mass of the Universe and its density $\rho\sim 10^{33}/10^{54}\sim 10^{-21}$ g/cm$^3$. We take into account now, that, as the bodies move away from each other at the two-fold distance, the force decreases four-fold, etc. We try to imitate the effect (on a body) of the gravitational force from the Universe in some direction. Even if we suppose the mean distance between the nearest stars to be 1 light year, then at the distance of 1 meter it is necessary to place the mass (we sum up to $2\cdot 10^{10}$) of

$$M_0\sim 25(1+1/4+1/9+\cdots) = 25\sum 1/n^2\sim 25\pi^2/6 < 50$$

grams. In fact, coefficient $\pi^2/6$ expresses some effective increase of the density at the observation line. To simulate the action of the "whole Universe" we can take a thick metal sphere with outer radius of 1 meter and make its thickness varying in the direction to the center (to imitate heterogeneities, we can make the needle-shaped structure near the inner radius).

Let the width of a solid sphere be $0.6$ meters, i.e. from the center up to $0.4$ meters there is a niche, and further, up to 1 meter, - the metal. Then a cylindrical column of radius $\sim 0.35$  cm will correspond to mass $M_0$ at density of $\sim 8.3$ g/cm$^3$. In reality, we should take into account the influence of stars in a cone, but not only in a cylinder. Though we also have a spherical metal cone, nevertheless, we shall estimate the orders of magnitudes. We shall break a cone into cylindrical layers, which arise as the new layers of stars are involved into consideration (Fig. 2.9).

Figure 2.9: The Mach principle and influence of the Universe.

Each new layer will be greater, than a preceding layer, by 6 stars. The distances from the center to the nearest boundary of each layer of stars can be found from the similarity of triangles: $R_i/1 = i/r$. Then we have $R'_i = \sqrt{i^2(1+r^2)}/r$. Therefore, the correction to a mass (we sum up to $2\cdot 10^{10}$) will be found as

$$m_0(1+{1\over 4}+\cdots )\biggl ( 1 + \sum_i {6\over {R'}_i^2}\biggr ) < M_0\biggl ( 1+ 6r^2 \sum_i {1\over i}\biggr )$$

$$\sim M_0\biggl ( 1 + 6 \cdot 10^{-5} \log{(2 \cdot 10^{10})}\biggr ) \sim M_0(1+0,02).$$

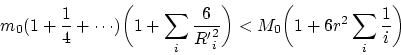
Thus, our construction is quite sufficient for taking into account the "whole Universe". Certainly, if the Universe is infinite, then the obtained harmonic series will diverge, and the construction will be inadequate. This, however, contradicts both GRT and the modern ideas.

Let now place the globules on a spring inside the sphere. To avoid the collateral effects, the air can be pumped out from the structure and, in addition, the globules can be isolated from the sphere by a thin vessel. Now, if we begin to spin up the sphere, then, according to the Mach principle, the centrifugal force should appear, and the globules will move apart of each other. In this case the centrifugal force must be the same, as though the globules themselves would rotate. It seems quite obvious, that this is impossible, since such an effect would be noticed still long ago. Thus, we return to absolute notions of acceleration, mass, space and time defined still by Newton. However, the described experiment could appear to be useful for determining the corrections to the static Newton's law of gravitation. In this case the globules should have sufficient freedom to move and to rotate, since the direction of action of correcting forces and moments of forces is unknown a priori.