The relativistic law for velocity addition

Recall that the kinematics does not study the causes of motion, but, for example, knowing the given velocities it finds the result of addition of these velocities. The issues of dynamics of particles (i.e. causes of motions) require independent consideration (see Chapter 4).

We begin with a remark concerning the relativistic law for velocity addition. For two systems participating in relative motion, the determination of their relative velocity causes no doubts (neither in classical physics nor in SRT). Let system $S_2$ be moving relative to system $S_1$ at speed $v_{12}$; similarly, let system $S_3$ be moving relative to $S_1$ in the same directions at speed $v_{13}$. In fact, the relativistic law for velocity addition defines the relative speed of that motion in which the observer does not participate himself: The speed of motion of system $S_3$ relative to $S_2$ is determined as

$$v_{23} = {v_{13} - v_{12}\over 1 - {v_{13}v_{12}\over c^2}}.$$ (1.5)

It is precisely this form (although usually $v_{13}$ is expressed in terms of $v_{12}$ and $v_{23}$), which discloses the real essence of this law: it tells what relative speed of systems $S_3$ and $S_2$ will be recorded by the observer in $S_1$, if the Einstein light-signal method is used for time synchronization and for measuring length. Actually, we have here the "law of visibility". (For the case of possible frequency dependence of light speed, this expression will change - see Appendixes).

Consider the following methodological remark. One rather strange kinematic notion from SRT is the non-commutativity of the relativistic law for velocity addition of non-collinear vectors. The non-commutativity property (and the fact, that the Lorentz transformations without rotations do not compose a group) is mentioned only briefly in some theoretical physics textbooks. By contrast, a similar property in quantum mechanics essentially changes the entire mathematical formalism and physically expresses a simultaneous immeasurability of non-commutating quantities.

It is seen from the general relativistic law of addition of velocities that

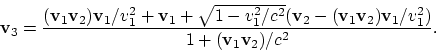$${\bf v}_3 = {({\bf v}_1{\bf v}_2){\bf v}_1/v_1^2 + {\bf v}_1... ...{\bf v}_2){\bf v}_1/v_1^2)\over 1 + ({\bf v}_1{\bf v}_2)/c^2}.$$ (1.6)

Clearly, the result depends on the order of transformation. For example, in the case of sequence

$$+v_1{\bf i}, -v_1{\bf i}, +v_2{\bf j}, -v_2{\bf j},$$

where ${\bf i}$, ${\bf j}$ are the unit vectors of the Cartesian coordinate system, we obtain a zero sum velocity, and for the other order of the same quantities

$$+v_1{\bf i}, +v_2{\bf j}, -v_1{\bf i}, -v_2{\bf j}$$

we obtain a non-zero sum velocity, which depends on $v_1$ and $v_2$ in a rather complicated manner. The successive application of transformations (of motions) of $v_1{\bf i}$ and $v_2{\bf j}$ results in

$${\bf v}_3 = v_1{\bf i} + \sqrt{1-v_1^2/c^2}v_2{\bf j},$$

and in the other order of $v_2{\bf j}$ and $v_1{\bf i}$ it results in

$${\bf v}'_3 = v_2{\bf j} + \sqrt{1-v_2^2/c^2}v_1{\bf i};$$

that is, we obtain different vectors (Fig. 1.21).

Figure 1.21: Velocity parallelograms in SRT.

In such a case, what can the decomposition of the velocity vector into components mean? First, the transfer of simplest, classical calculation techniques (the commutative algebra) to relativistic (non-commutative) equations is illegal: even the solution of vector equations in a component-by-component manner requires additional postulates, complications or explanations. Second, a simple application of the methods of classical physics (such as the principle of virtual motions, the variation methods, etc.) is impossible. In this case, even a "zero" had to be "individualized": the number of "zero" quantities, composed of some vector combination, should be equal to the number of "zero" quantities composed of a mirror vector combination. Hence, the theory of fluctuations would also require additional substantiation in such a case. Thus, contrary to the statement "on the simplicity and elegance of SRT", the correct justification of even simplest procedures would require introducing many artificial complications and explanations (which are absent in the textbooks).

Consider the logical contradiction of the relativistic law of velocity addition for the example of one-dimensional case. Let us have a balance in the form of a horizontal groove with a horizontal transverse pivot at the middle. Two identical balls of mass $m$ will roll along a groove from the pivot to different sides (Fig. 1.22).

Figure 1.22: The law of addition of velocities and the paradox of a balance.

To avoid discussing properties of the relativistic mass, we shall proceed as follows. Let the balance pivot be frictionless except when the balance is in the horizontal position (the "dead point"). At this position, the threshold of the friction force does not allow the balance to rotate due to any possible small difference between the relativistic masses of the balls. But this sensitivity threshold cannot prevent the balance from rotating off the "dead point" in the absence of one of balls - it will fall downwards. Let the velocities of balls in the system be equal in magnitude. Then the balls in this system will simultaneously reach the edges of the groove and fall downwards, so that the balance will be kept at the horizontal position. Consider now the same motion in the system, relative to which the balance are moving at speed $V$. Let be $V \rightarrow c$ only, but $v \ll v_s$, where $v_s$ is the speed of sound for the groove material. Then the balance can be considered as absolutely rigid (we can ignore acoustic waves). According to the relativistic law of addition of velocities,

$$v_1 = {V-v\over 1-vV/c^2}~, ~~~~~ v_2 = {V+v\over 1+vV/c^2}~.$$

The motion of a middle point at speed

$${v_1 + v_2\over 2} = V{1 - v^2/c^2\over 1 - v^2V^2/c^4} < V$$

always lags the motion of the balance. Thus, the ball moving against the direction of motion of the balance will fall down first. As a result, the equilibrium will be violated, and the balance will begin to rotate. So, we have a contradiction with first observer's data. Will the observer be hit if he will stands under the right-hand part of the balance?

Will the Lorentz transformation laws be able to describe successive transitions from one inertial system to another, and does the relativistic law of addition of velocities correspond to real velocity variations? Certainly not. First, recall the meaning of the relativistic law of velocity addition. It must prove that the addition of any motions cannot lead to a speed greater than light speed. What is the manner (sense) in which motions are added in this case? For example, the Earth moves relative stars (factually, there exists the first reference system), a spacecraft flies up from the Earth with large velocity (in fact, the second reference system is "created"), then, another spacecraft flies up from the first spacecraft (factually, the third reference system is "created"), and so on. It is just the meaning for consecutive transformations. Then the following question no longer arises: in the relativistic law of velocity addition, which velocity must be considered as the first one, and which velocity is the second one (This is important for non-commutative transformations). All the examples in this Section have this meaning.

Let us consider now the Lorentz transformation law for arbitrary directions of motion:

$${\bf r}_1 = {\bf r} + {1\over V^2}\biggl ( {1\over \sqrt{1-V... ...\biggr ) ({\bf rV}){\bf V} + {{\bf V}t\over \sqrt{1-V^2/c^2}},$$

$$t_1 = {t + ({\bf rV})/c^2\over \sqrt{1-V^2/c^2}}.$$

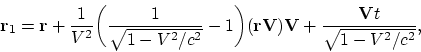
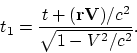
It can easily be verified, that the successive application of the relativistic law of velocity addition (1.6) to quantities

$$v_1{\bf i}, ~~ v_2{\bf j}, ~~ -v_1{\bf i} - v_2\sqrt{1-v_1^2/c^2}{\bf j}$$ (1.7)

will give a zero. To an arbitrary vector ${\bf r} = x{\bf i} + y{\bf j}$ we apply the Lorentz transformation laws successively with the same set of velocities. Then we have:

$${\bf r}_1 = {x+v_1t\over \sqrt{1-v_1^2/c^2}}{\bf i} + y{\bf j},$$

$$t_1 = {t+xv_1/c^2\over \sqrt{1-v_1^2/c^2}}.$$

Further, we have:

$${\bf r}_2 = {x+v_1t\over \sqrt{1-v_1^2/c^2}}{\bf i} + {y\sqr... ...xv_1v_2/c^2\over \sqrt{1-v_1^2/c^2}\sqrt{1-v_2^2/c^2}}{\bf j},$$

$$t_2 = {t+xv_1/c^2+yv_2\sqrt{1-v_1^2/c^2}/c^2\over \sqrt{1-v_1^2/c^2}\sqrt{1-v_2^2/c^2}}.$$

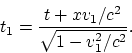
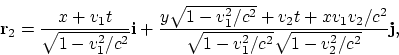
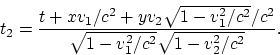
We shall not write down the expressions for $r_3$ and $t_3$ in the explicit form because of their awkwardness. However, using graphical programs, we can be convinced of the following properties:
1) In the new system, the initial time is desynchronized at any point of space except the coordinate origin.
2) The time intervals have changed: $dt_3\ne dt$; that is, we got into a new moving system, rather than into the initial resting one. Therefore, in the textbooks, as a minimum, the meaning of the Lorentz transformation laws or of the relativistic law of velocity addition is uncovered rather incorrectly.
3) Line segments occur to be not only changed in length, but also turned around. We can easily be convinced of this, if we find numerically the angle of rotation; i.e. the difference

$$\alpha = \arctan\Biggl ( {y_3[x(1),y(1),t]-y_3[x(0),y(0),t]\... ...Biggr ) - \arctan\Biggl ( {y(1)-y(0)\over x(1)-x(0)}\Biggr ) .$$

These properties can be discussed mathematically in terms of the "pseudo-Euclidean character of the metric" as much as you like. However, physically the situation is quite simple. These properties prove the non-objective (i.e. only illusory) character of the Lorentz transformation laws and of the relativistic law of velocity addition, and their disagreement with each other. Indeed, since we have successively passed from one inertial system to another, and the rotation implies the non-inertial character of a system, SRT itself escapes the limits of its own applicability; i.e., it is inconsistent. If this rotation were real, this would imply a non-objective character of the inertial system notion (since the result would depend on the method of transition to the given system) and, as a consequence, the lack of a proper basis for SRT to exist.

Let us try to clear up why it is that treatments from the textbooks result in disagreement between two expressions, the relativistic law of velocity addition and the Lorentz transformation laws, in spite of the fact that the first expression is derived from second one. Recall the following derivation for the example of one-dimensional mutual motion of systems $K$ and $K'$. Proceeding from the Lorentz transformation laws

$$x_1 = {x+Vt\over \sqrt{1-V^2/c^2}}~, ~~~~ t_1 = {t+Vx/c^2\over \sqrt{1-V^2/c^2}}$$

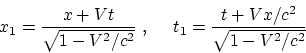
we divide the differential $dx_1$ by $dt_1$ with regard to definitions $v=dx/dt$ and $v_1=dx_1/dt_1$ and obtain:

$$v_1 = {v+V\over 1+vV/c^2}.$$

This indicates the following things:
1) The observer is at the origin of system K and measures the distance $x$ to the studied body in its system $K$.
2) He considers time $t$ to be universal in his system and determines the velocity of a body in his system $v=dx/dt$.
3) He measures speed $-V$ of system $K'$ with respect to $K$ using his own (!) time $t$, and considers the relative velocities of systems to be mutually opposite in direction. This observer cannot measure any other thing: the summary velocity $v_1$ is a computable quantity. Thus, we came to the treatment [49] given above: the relativistic law of velocity addition determines the velocity of that relative motion, in which the observer does not participate by himself. This effect is not real, but only apparent (when we use some particular rules of SRT). In the essence of the formula, we cannot simply pass to the second substitution for determining $v_2$, though, formally, any arbitrary number of velocity values can be sequentially substituted into the expression for the relativistic law. In the case of addition of motions along a single straight line, the classical property of commutativity conserves, and the contradiction is veiled over. But if the velocity vectors are non-collinear, then item 3) becomes untrue, and the inconsistency and disagreement of the law of velocity addition and Lorentz transformation laws are immediately exhibited.

But we can apply another approach to the example discussed previously: we shall search for the sequence of three transformations of velocities that retains the initial time in the Lorentz transformation laws invariant. Then it can easily be verified that, instead of (1.7), a single succession can be taken:

$$v_1{\bf i}, ~~ v_2{\bf j}, ~~ -v_1\sqrt{1-v_2^2/c^2}{\bf i} - v_2{\bf j} .$$ (1.8)

However, at first, the turning of segments remains. Second, a new set of velocities does not satisfy, in the given succession, the law of velocity addition, i.e. factually there changes the order of substitution of the velocities $v_1$ and $v_2$ in the law of velocity addition (that is inconsistent with the essence of this law). Therefore, the contradictions are not eliminated in this case as well. The Thomas precession is an example of SRT inconsistency also: starting from the sequence of inertial systems (moving rectilinearly and uniformly), the resulting rotation of objects is suddenly obtained (principally noninertial motion). Thus, the passage from the Lorentz transformations (outlined in standard textbooks) of "mathematical space" $1+1$ ($t+x$) to the Lorentz transformations of $1+2$ "space" (or $1+3$) leads to physical contradictions.

Many intuitively clear properties of physical quantities lose their sense in SRT. For example, the relative velocity ceases to be invariant. The particles, flying away along the same straight line at various velocities, form in SRT a complicated "fan of velocities" for a moving system. The isotropic velocity distribution in SRT ceases to be the same for the other moving system. No declared simplification does exist in SRT in reality.

The impossibility of existence of velocities $v>c$ in no way follows from SRT. And the addition, that this statement relates to the signal transmission rate only, is only artificial addition (because of existence of obvious counterexamples to the extended treatment). However, the notion of signal (information) remains insufficiently determinate even with a similar addition. For example, while receiving a signal from the flare of supernova, are we not sure that the same information "is contained" at the diametrically opposite distance from the supernova (that is, we know about it at velocity of $2c$)? Or this is not information? Therefore, SRT can only deal with the information on a material carrier of electromagnetic nature propagating in vacuum sequentially through all points of space from the signal source to a receiver.

Let us make some comment on "astonishingness" of the relativistic law of "addition" of velocities, which allows to exchange light signals even for the algebraic sum of velocities greater than $c$. We pay attention to the obvious fact: for exchanging information the signals should be sent necessarily in the direction of an object, rather than in the opposite direction. Therefore, there is nothing surprising in exchanging the signals, where in the classical case it occurs also that, as a result of formal addition of velocities, $v_1+v_2>v_{signal}$. Let two airplanes to take off from the aerodrome $O$ at velocities of $0.9v_{sound}$ and fly away from each other in the opposite directions of axis $X$ (the relative velocity is $1.8v_{sound}$). Whether the exchanging of signals between them is possible? Certainly yes! Because the sound wave propagates in air irrespective of the velocity of source $S_1$ at signal issuing time, the first airplane (which has sent a signal) will catch up the wave front propagating in the positive direction of axis $X$, whereas the second airplane will "compete" with the wave front propagating in the negative direction of axis $X$. Both airplanes are moving slower as compared to propagation of corresponding wave front sections nearest to them (see Fig. 1.23).

Figure 1.23: Exchange of a signal.

Thus, the sum of velocities is compared (in a complicated manner), in reality, with quantity $2v_{sound}$, rather than with the speed of sound (and for light - with the value of $2c$).

It is obvious also that physical restrictions on the value of speeds cannot be applied by mathematics (by the fact that in some expressions there exists a negative value under the radical sign). It should be remembered that all SRT expressions are introduced with use of a light signal exchange (the method of Einstein's synchronization). But if a body moves faster than light long since, it simply cannot be caught up by signal sent in pursuit. In a similar manner, a synchronization can be made with use of sound (expressions with radicals could be written), but the impossibility of supersonic speeds in no way follows from here at all.