Einige relativistische Lösungen und Folgen

Betrachten wir das Paradoxon von Kräftetransformation. Mögen wir zwei ruhende ungleichnamige Ladungen $e_1$ und $e_2$, die durch zwei parallelen Ebenen geteilt sind, die sich in der Entfernung $L$ (Abb. 4.4) voneinander befinden.

Abbildung 4.4: Paradoxon von Kräftetransformation.

Infolge der Anziehung zueinander befinden sich die Ladungen in minimaler Entfernung $L$ voneinander. (Sie befinden sich im indifferenten Gleichgewicht bezüglich des Systems von Ebenen.) Machen wir eine Kerbe auf der Ebene unter jeder Ladung oder stellen daneben Beobachter. Wir werden jetzt dieses System von Ladungen aus dem relativistischen Weltraumschiff beobachten, das sich mit der Geschwindigkeit ${\bf v}$ bewegt. Mag $\theta$ - der Winkel zwischen zwei Vektoren ${\bf v}$ und ${\bf L}$ sein. Bei der Bestimmung der elektromagnetischen Kräfte, die zwischen diesen Ladungen im Bezugssystem des Weltraumschiffes [17] wirken, werden wir uns für tangentiale Komponenten von Kräften interessieren, d.h., für die Komponenten von Kräften längs der Ebenen Auf die Ladung $e_1$ wirkt die Kraft

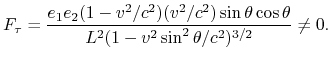$$F_{\tau} = {e_1e_2(1-v^2/c^2)(v^2/c^2)\sin\theta\cos\theta\over L^2(1-v^2\sin^2\theta/c^2)^{3/2}}\ne 0.$$ (4.1)

Folglich versetzen sich die Ladungen von ihrer ursprünglichen Lage. Mögen die Kugeln gewaltige Ladungen haben, $L$ wird klein ( $L\rightarrow 0$)sein, und $v$ wird groß ( $v\rightarrow c$)sein. Es sollen die Beobachter die Kugeln mit dünnen Fäden festhalten. Ob sie zerreißen? Die Frage hängt vom Beobachtungssystem ab. Wer von den Beobachtern hat recht? So haben wir den nächsten Widerspruch der SRT.

Betrachten wir jetzt manche Einzelaufgaben. Methodisch paradox ist die Beschreibung der Bewegung des geladenen $e$ Teilchens mit Masse $m_0$ im konstanten homogenen elektrischen Feld $E_x=E$ (s. [34]). In der klassischen Physik ist die Trajektorie bei $v_y=v_0$ die Parabel

$$x = eEy^2/(2m_0v_0^2),$$

in der SRT die Kettenlinie

$$x = {m_0c^2\over eE}\biggl ( \cosh\biggl [ {eEy\over m_0v_0c}\biggr ] - 1\biggr ).$$

Aber bei dem großen $y$ ist die relativistische Trajektorie nah der Exponente, d.h., sie ist steiler als die Parabel. Was tun mit der Idee der Vergrößerung von Trägheit (Masse)des Körpers mit Geschwindigkeit? Wenn man sogar annimmt, dass sich das Teilchen ungeachtet der gewissen großen Steilheit auf der Trajektorie langsamer bewegt, anhand welcher Kräfte verlangsamte sie längs der Achse $y$? Die Kraft $F_y=0$ und in der SRT zeigt sie sich auch nicht: $F'_y=0$. Die Größe der Angangsgeschwindigkeit $v_y=v_0$ kann nicht relativistisch sein (und bleibt als solche).

Seltsam ist das Gleichgewicht der Energie für das relativistische Weltraumschiff [33]:

$$m\cosh\theta + M_2\cosh(d\theta) = M_1.$$

Bei großer Stoßgeschwindigkeit ( $\theta=\tanh(v/c)$) soll die Bedingung für die endlichen Werte von der Anfangsmasse $M_1$ und der endlichen Masse $M_2$ erfüllt werden: die Masse eines einzelnen Stoßes $m\rightarrow 0$ (für die Übereinstimmung der SRT). Diese Größe wird doch nur vom technischen Aufbau des Weltraumschiffes bestimmt: es gibt keine prinzipiellen Beschränkungen.

Eine der Ableitungen von Einstein vom Verhältnis $E=mc^2$ ist nicht genug begründet. In dieser Ableitung wird der Prozess der Absorption von zwei symmetrischen Lichtimpulsen durch Körper aus Sicht von zwei Beobachtern betrachtet, die sich bezüglich einander bewegen. Der erste Beobachter ruht bezüglich des Körpers, der zweite bewegt sich senkrecht zum Licht (Abb. 4.5).

Abbildung 4.5: Zur Ableitung der Formel $E=mc^2$.

In der SRT heißt es, dass das Licht im Voraus von der Bewegung des Beobachters eben mit der Geschwindigkeit $v$ wissen soll und so den Impuls erhalten, dass sich die Geschwindigkeit des Körpers in diesem zweiten System nicht ändert, und nur seine Masse wird verändert. Was soll mit den Lebedew-Lichtdruckexperimenten geschehen (und mit der heutigen allgemeingültigen Vorstellung), wenn sich eben die beobachtende Geschwindigkeit des Körpers bei der Impulsübertragung vom Licht änderte? Und was wird mit dem Impuls, wenn wir absolut absorbierende unebene (schräge) Ebenen haben? Nach den angeführten Abbildungen ist es auch nicht klar, ob wir mit dem realen transversalen Licht (mit dem heutzutage gültigen Modell, darunter in der SRT) oder mit dem mystischen longitudinal-transversalen Licht (für die SRT-Rettung) zu tun haben.

Ziemlich seltsam in der heutigen SRT-Version ist die Differenz der Masse der Gesamtstrahlung in Abhängigkeit vom Impuls des Systems:

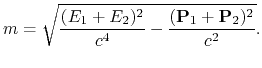$$m = \sqrt{{(E_1+E_2)^2\over c^4} -{({\bf P}_1+{\bf P}_2)^2\over c^2}}.$$ (4.2)

Und wenn wir den Impuls (die Richtung) einzelner Photonen durch Spiegel tauschen werden? Wir werden dabei den Gravitationsmittelpunkt des Systems festlegen. Wo wird er lokalisiert, und wie wird die Struktur in der Nähe des Feldes sein? Ob dieser Mittelpunkt springen, verschwinden und wieder zum Vorschein kommen wird? Wenden wir die angeführte SRT-Formel (4.2) für die Bestimmung der Masse der Gesamtstrahlung von zwei Photonen an, die sich unter dem willkürlichen Winkel zerstreuen, und betrachten wir die Strahlung, die aus einem Mittelpunkt auseinanderläuft (Abb. 4.6).

Abbildung 4.6: Masse der Photonenkombination.

In Abhängigkeit von der Paargruppierung von Photonen kann man dann unterschiedliche Gesamtmasse des ganzen Systems erhalten (ob es nicht nötig wird, negative Massen für die „Erklärung“ aller möglichen Variationen der Masse künstlich einführen?) In der ART soll man die Vorgeschichte der Erzeugung von Strahlung für die Bestimmung der Lokalisierung ihres Gravitationsmittelpunktes und die ganze unbekannte Raumzeitstruktur des elektromagnetischen Feldes für die richtige Beschreibung einer ganz anderen Erscheinung – der Gravitation - berücksichtigen. Unendlich kompliziert!